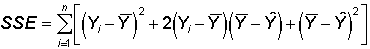The basic form of the proof is to calculate the sum of squared errors for an arbitrary estimate and then to show that it necessarily includes all the sum of squared errors for the mean plus some additional error. In that case, we obviously do best to use the mean.

We will represent an arbitrary estimate by 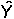and the mean is of course defined by

For an arbitrary estimate, the sum of squared errors is

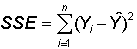
Obviously, so we can add this representation of zero within the parentheses without changing the sum of squared errors. That is,

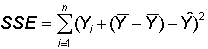
Rearranging the terms slightly and regrouping, we get
Squaring inside the summation gives

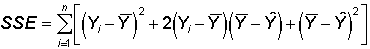
Breaking the sums apart yields

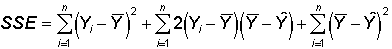
The last term contains no subscripts so the sum can be replaced with

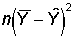
and the factor with no subscripts in the second term can be moved outside the summation giving

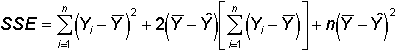
The bracketed term is the sum of the deviations about the mean and must therefore equal zero. So, the above equation reduces to

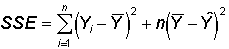
If our model estimate equals the mean, then and the last term in the prior equation is zero. Thus, when the model estimate is the mean,

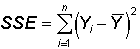
and if the model estimate equals anything other than the mean, the sum of squared errors would be increased by

Hence, the mean minimizes the sum of squared errors; any other estimate necessarily gives a larger sum of squared errors.