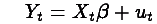
|| GARCH EXAMPLE || TGARCH EXAMPLE || SGARCH EXAMPLE || GARCH-M EXAMPLE ||
For details about the GARCH process see Time Series Analysis, Chapter 21, Section 2, by James D. Hamilton (ISBN 0-691-04289-6, Princeton U Press, 1994).
The GARCH(p,q) process models the residual of a time series regression. Let
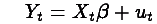
The residual is modelled as
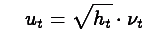
where
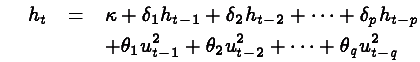
and where in the standard GARCH model
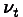has the unit Normal density:
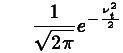
In addition, to preserve stationarity the following constraints are placed on the coefficients:
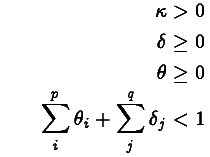
Other constraints are possible. For example changing the last constraint to
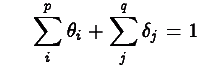
results in an IGARCH model.
The GARCH program is written in the GAUSS programming language and uses Aptech System's Constrained Maximum Likelihood applications module. It generates maximum likelihood estimates of the GARCH(p,q) model subject to the GARCH constraints.
The example produces estimates and Wald confidence limits for the GARCH(1,1) process for a 22 year time series of monthly observations of a well-known index of securities.
The Constrained Maximum Likelihood applications program permits general linear and nonlinear constraints, both equality and inequality. The GARCH constraints described above are sufficient but not necessary. Thus you may wish to place other constraints on your model (see Daniel B. Nelson and Charles Q. Cao, 1992, "Inequality Constraints in the Univariate GARCH Model", Journal of Business and Economic Statistics, 10:229-235). The GARCH program can be easily modified to place the constraints these authors suggest, as well as any other constraints you wish.
Let
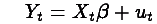
As with the GARCH(p,q) process the TGARCH(p,q) process models the residual as
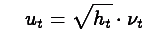
Rather than giving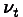
a unit Normal distribution, TGARCH instead
applies the
t-distribution:
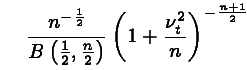
The extra parameter, n, is a measure of platykurtosis,
i.e., the "fatness" of the tails of the distribution
of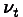
The TGARCH program is written in the GAUSS programming language and uses Aptech System's Constrained Maximum Likelihood applications module. It generates maximum likelihood estimates of the TGARCH(p,q) model subject to the GARCH constraints.
This example produces estimates and Wald confidence limits for the TGARCH(1,1) process for the same time series used in the GARCH(1,1) example above:
The TGARCH(1,1) results for the coefficient estimates are quite similar to the GARCH(1,1) results. The likelihood ratio test of the GARCH vs the TGARCH models is 9.8194 with 1 degree of freedom, thus supporting a hypothesis that the time series is platykurtotic, i.e, "fat-tailed".
Let
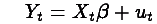
The SGARCH(p,q) process models the residual as
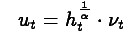
where
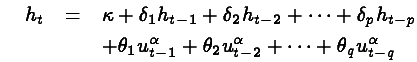
and where
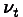is specified to
have a stable density.
The stable density doesn't have a simple
mathematical description, so instead the
log of the characteristic function is used:
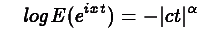
See W.H. DuMouchel, 1973, "Stable Distributions in Statistical Inference: 2. Information from Stably Distributed Samples," Journal of the American Statistical Association, 70:386-393.
For the GARCH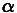 
= 2.
However, for the SGARCH model
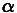is a parameter to be estimated.
The SGARCH program is written in the
GAUSS programming language
and uses Aptech System's
Constrained Maximum Likelihood
applications module. It generates maximum likelihood estimates
of the SGARCH(p,q) model subject to the GARCH constraints.
The initialization of the GARCH process is different for the SGARCH program than it is for the GARCH and TGARCH programs. In the GARCH and TGARCH programs, the initial values are set to the empirical variance of the time series, as suggested by Tim Bollerslev, 1986, "Generalized Autoregressive Conditional Heteroskedasticity", Journal of Econometrics, 31:307-327.
In SGARCH, however, this would be inappropriate and instead R initial observations are fit to the stable distribution and the resulting scale parameter is used to determine the initialization of the GARCH process. The example produces estimates and Wald confidence limits for the SGARCH(1,1) process for the same time series used in the GARCH(1,1) example above:
The likelihood ratio test of the SGARCH vs the GARCH models is 16.1546 with 1 degree of freedom, thus also supporting a hypothesis that the time series is platykurtotic, i.e, "fat-tailed". The SGARCH and TGARCH models are not nested and so the likelihood ratio test cannot be used to distinguish these models. However, the evidence that the time series is platykurtotic is rather solid.
The GARCH-M model adds the heteroskedastic term directly into the equation:
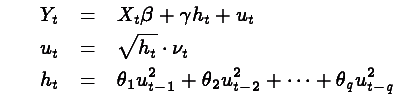
This new term is introduced to measure the response of the
dependent variable to the "volatility" of the time series.
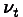here is given the Normal
distribution, though stable and t-distributions could also be
used.
The GARCH-M program is written in the
GAUSS programming language
and uses Aptech System's
Constrained Maximum Likelihood
applications module. It generates maximum likelihood estimates
of the GARCH-M(p) model subject to the constraints that
the GARCH-M terms are positive.
The example produces estimates and Wald confidence limits for the GARCH-M(1) process for the same time series used in the GARCH(1,1) example above:
This model was difficult to estimate. I had to start from different starting points to get the results shown here because a saddle point was encountered.
Another new GAUSS feature is also illustrated in this example. C source code is provided in the example for computing the do loop in the log-likelihood function. Instructions are included in the example file for compiling and using the function through the foreign language interface.
The likelihood ratio test of the GARCH-M vs the GARCH model is 4.2347 with 1 degree of freedom is not statistically significant and thus we fail to find evidence for a response to volatility in the example time series.