|
High Performance Scientific Computing
AMath 483/583 Class Notes Spring Quarter, 2013 |
Due Wendesday, June 12, 2013, by 11:00pm PDT.
The goals of this project are to:
See also:
Create a new subdirectory project in your repository for the codes you create.
PART 1
Create a subdirectory project/part1 for this part.
In the last part of Homework 6, you wrote an MPI code to compute a Trapezoid approximation to an integral by splitting the original interval up into nsub = num_procs - 1 subintervals. The master Process 0 farmed these out to the remaining processes and collected the results.
Modify your code to make a new version test3.f90 that allows nsub to be set to a value larger (or smaller) than num_procs - 1. In this case the master process should send out subintervals to the worker processes until all the work is done. This will require doing something similar to what is done in the sample code $UWHPSC/codes/mpi/matrix1norm2.f90 to keep track of which subintervals have been handled.
Have Process 0 read in the number of subintervals with the lines:
print *, "How many subintervals? " read *, nsuband then broadcast this value to the other processes.
Test that your code works both when the number of subintervals is smaller or larger than the number of processes specified with mpiexec.
If the code is run with a single process then it should halt with an error message (since there are no workers to compute the integral over subintervals in this case).
Provide a Makefile that compiles using mpif90 and runs the code by default with 4 processes, as in Homework 6.
Sample output
Your code should produce output similar to this, for example...
$ make test3 mpif90 -c functions.f90 mpif90 -c quadrature.f90 mpif90 -c test3.f90 mpif90 functions.o quadrature.o test3.o -o test3.exe mpiexec -n 4 test3.exe Using 4 processes How many subintervals? 2 true integral: 6.00136745954910E+00 fevals by Process 0: 0 fevals by Process 1: 1000 fevals by Process 2: 1000 fevals by Process 3: 0 Trapezoid approximation with 2000 total points: 6.00125232481036E+00 Total number of fevals: 2000 $ make test3 mpiexec -n 4 test3.exe Using 4 processes How many subintervals? 7 true integral: 6.00136745954910E+00 fevals by Process 0: 0 fevals by Process 1: 3000 fevals by Process 2: 2000 fevals by Process 3: 2000 Trapezoid approximation with 7000 total points: 6.00135820753458E+00 Total number of fevals: 7000 $ make test3 NUM_PROCS=1 mpiexec -n 1 test3.exe *** Error: need to use at least two processes
PART 2
Create a subdirectory project/part2 for this part.
Monte Carlo methods are often used to estimate the values of definite integrals in high dimensional spaces since traditional quadrature methods based on regular grids may require too many points.
The files in $UWHPSC/codes/project/part2 contain much of what is needed to experiment with a Monte Carlo approximation to the integral
\(\int_{a_1}^{b_1} \int_{a_2}^{b_2} \cdots \int_{a_d}^{b_d} g(x_1,x_2,\ldots,x_d) dx_1~dx_2~\cdots~dx_d\)
over a rectangular region in \(d\) space dimensions. The Monte Carlo approximation to the integral is given by
\(\frac V N \sum_1^N g(x_1^{[k]},x_2^{[k]},\ldots,x_d^{[k]})\)
where \((x_1^{[k]},x_2^{[k]},\ldots,x_d^{[k]})\) is the k’th random point and \(V = (b_1-a_1)(b_2-a_2)\cdots(b_d-a_d)\) is the volume of the rectangular region of integration.
The main program in test_quad_mc.f90 is set up to experiment with a simple integral with varying number of Monte-Carlo points.
What is missing is the module quadrature_mc.f90. Create this module, containing a function quad_mc with the calling sequence:
quad_mc(g, a, b, ndim, npoints)that returns a Monte Carlo approximation to the integral, where:
- g is the function defining the integrand. g takes two arguments x and ndim, where x is an array of length ndim, the number of dimensions we are integrating over. (See the example in the functions.f90 module.)
- a and b are arrays of length ndim that have the lower and upper limits of integration in each dimension.
- ndim is the number of dimensions to integrate over.
- npoints is the number of Monte Carlo samples to use.
The random number generator should be called only once to generate all the points needed and then the function g evaluated at appropriate points. Note that you will need npoints*ndim random numbers since each point x has ndim components.
Allocate appropriate size arrays to manage this.
Note that the function \(g(x)\) specified for this test is very simple so that the true solution can be easily computed in any number of dimensions.
\(g(x) = x_1^2 + x_2^2 + \cdots + x_d^2\)
The test program in test_quad_mc.f90 computes the exact integral of this over any rectangular region. Convince yourself this is right.
Once you have provided a suitable module as described above, running this code should give results like the following:
$ make plot gfortran -c random_util.f90 gfortran -c functions.f90 gfortran -c quadrature_mc.f90 gfortran -c test_quad_mc.f90 gfortran random_util.o functions.o quadrature_mc.o test_quad_mc.o -o test.exe ./test.exe Testing Monte Carlo quadrature in 20 dimensions True integral: 1.95734186666667E+08 seed1 for random number generator: 12345 Final approximation to integral: 1.95728471073896E+08 Total g evaluations: 1310720 python plot_mc_quad_error.pyA file mc_quad_error.txt should be created with the estimate of the integral computed with varying number of random points and the error in each.
A plot of these results should also be created as mc_quad_error.png, that looks like this:
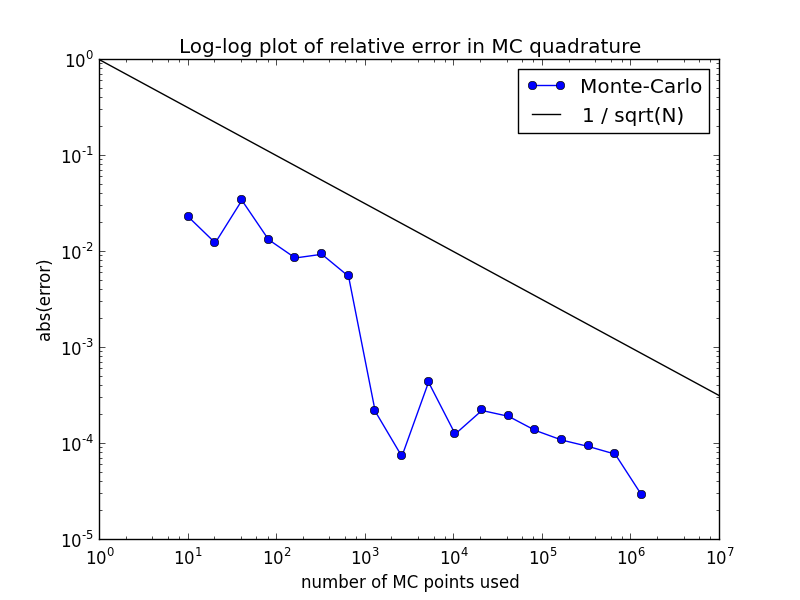
The test problem is set up to estimate a 20-dimensional integral. Note that the relative error is plotted, which gives an indication of the number of correct digits. (Note that the absolute error is about 2e8 times larger for this problem!)
Note: This problem should be quite easy; the code needed for quad_mc should be short. The main purpose of this problem is to illustrate the basic structure of such a code, which you can follow in the next problem.
PART 3
The sample program $UWHPSC/codes/project/part3/laplace_mc.py can be run from IPython to illustrate how a random walk on a lattice can be used to generate an approximate solution to the steady-state heat equation at a single point. This is described in more detail in the section Monte Carlo methods for the steady state diffusion equation.
Note that there is a parameter plot_walk that is set to True for this demo. If you set it to False and execute the code, then it will take many more walks and print out the approximations as it repeatedly doubles the number of walks taken.
Using this as a model, write a Fortran code to approximate the solution to Laplace’s equation at a single point \((x_0,y_0)\) using the random walk approach.
The module $UWHPSC/codes/project/part3/problem_description.f90 is a starting point.
Supplement this with the following:
- A module mc_walk.f90 containing two subroutines
- subroutine random_walk(i0, j0, max_steps, ub, iabort) based on the Python function random_walk. In the Fortran case ub should be an output variable with the value of u at the boundary point reached, in the case when the walk successfully reached the boundary. In this case the subroutine should return iabort = 0. If the walk did not reach the boundary after max_steps, then ub can be anything, but return iabort = 1 in this case.
- subroutine many_walks(i0, j0, max_steps, n_mc, u_mc, n_success) based on the Python equivalent. In this case u_mc should be an output variable with the average value of u on the boundary computed based on the successful walks, and n_success is an output variable telling how many were successful.
- Add a module variable nwalks to this module that is initialized to 0 in the main program and incremented by one each time random_walk is called.
- A main program named laplace_mc.f90 that does something similar to the main program in the Python code. In particular it should:
- Set x0, y0, i0, j0, max_steps as in the Python. You should use what’s needed from the module problem_description.f90.
- Initialize the random number generator. You can use the random_util.f90 module from Part 2 for this. Set seed1 = 12345.
- Intialize nwalks = 0 and print out at the end the value, which should be the total number of times random_walk was called.
- Call many_walks first with u_mc = 10 and then have a loop to repeatedly double the number of samples and print out the estimate of u and the relative error after each doubling.
- In addition, it should write the total number of walks, the estimate of u and the relative error each doubling to a file named mc_laplace_error.txt with the same format as the file mc_quad_error.txt in Part 2.
- A python script plot_mc_laplace_error.py based on the plotting script from Part 2 to produce a log-log plot of the results.
- A Makefile so that make plot will produce the png file.
The Fortran code does not need to include an option for plotting the walks, that was just for demo purposes.
Note that the main program and each subroutine will have to use various variables or subroutines from other modules.
Sample output
$ make plot gfortran -c random_util.f90 gfortran -c problem_description.f90 gfortran -c mc_walk.f90 gfortran -c laplace_mc.f90 gfortran random_util.o problem_description.o mc_walk.o laplace_mc.o -o test.exe ./test.exe seed1 for random number generator: 12345 10 0.377000000000000E+00 0.162222E+00 20 0.408125000000000E+00 0.930556E-01 40 0.452875000000000E+00 0.638889E-02 80 0.436125000000000E+00 0.308333E-01 160 0.440656250000000E+00 0.207639E-01 320 0.468687500000000E+00 0.415278E-01 640 0.460773437500000E+00 0.239410E-01 1280 0.455091796874999E+00 0.113151E-01 2560 0.455277343749997E+00 0.117274E-01 5120 0.455505371093748E+00 0.122342E-01 10240 0.456198974609378E+00 0.137755E-01 20480 0.454078369140635E+00 0.906304E-02 40960 0.450970458984394E+00 0.215658E-02 Final approximation to u(x0,y0): 4.50970458984394E-01 Total number of random walks: 40960 python plot_mc_laplace_error.pyNote that with max_steps = 100*max(nx,ny) all of the walks successfully reached the boundary. You might try with a smaller value such as max_steps = 10 in which case many walks will fail. In this case you might see results like the following (Note that the original results shown here were incorrect!)
seed1 for random number generator: 12345 4 0.697500000000000E+00 0.550000E+00 8 0.632500000000000E+00 0.405556E+00 17 0.608529411764706E+00 0.352288E+00 31 0.623548387096774E+00 0.385663E+00 71 0.622042253521127E+00 0.382316E+00 134 0.616623134328358E+00 0.370274E+00 268 0.623619402985075E+00 0.385821E+00 553 0.620099457504520E+00 0.377999E+00 1092 0.623298992673990E+00 0.385109E+00 2184 0.622995650183145E+00 0.384435E+00 4416 0.624125339673914E+00 0.386945E+00 8765 0.625060182544217E+00 0.389023E+00 17623 0.624690319468906E+00 0.388201E+00 Final approximation to u(x0,y0): 6.24690319468906E-01 Total number of random walks: 40960The total number of walks nwalks is the same, but fewer were used in each estimate of the solution.
PART 4
Required only of 583 students
Parallelize the code from Part 3 using MPI. Do this as follows:
Modify the main program to call MPI_INIT and MPI_FINALIZE. Note that with MPI, we must call MPI_INIT as the first statement in the main program, so every process is running the same code, and every process will call the subroutine many_walks. See $UWHPSC/codes/mpi/quadrature for an example of how Simpson’s method might be implemented in MPI.
In the main program, use:
seed1 = 12345 seed1 = seed1 + 97*proc_num ! unique for each process call init_random_seed(seed1)so that each process will generate a unique set of random numbers.
Modify subroutine many_walks so that Process 0 is the master whose job is to farm out all of the n_mc walks requested to each of the other processes. Follow the master-worker paradigm for this. This is a sensible way to try to do load balancing since some walks will take many more steps than others. (It would be better to ask each worker to do some number of walks greater than 1 each time so that there is less communication, but let’s keep it simple.)
Note that the master does not have to send any data to a worker, just an empty message requesting another walk, so it could send MPI_BOTTOM and use tag = 1 to indicate this is a request for another walk. Use tag = 0 to indicate to a worker that it is done.
The worker will have to receive from the master with MPI_ANY_TAG and then check status(MPI_TAG) to see what it needs to do.
If another walk is requested, the worker should call random_walk and then send back to the Master the result as a single data value of type MPI_DOUBLE_PRECISION. For this message set the tag to the value of iabort that was returned from the call to random_walk so that the Master knows whether to include this walk in the accumulated Monte Carlo result.
Recall that with MPI every process is executing the same code but that all data is local to a process. So the basic structure of the main program can remain the same. Every process will execute the loop that repeatedly increases the size of n_mc and every process will call many_walks. But only the master process will return values of u_mc and n_success that are sensible, and so this process should update u_mc_total and print out the values to the screen and the file mc_laplace_error.txt.
The module variable nwalks that is incremented in random_walk will be local to each process. In the main program, at the end have each process print out how many walks it took and use MPI_REDUCE to compute the total number of walks taken by all processes and have Process 0 print this value.
Create a Makefile that works for this by combining aspects of those from Part 1 (for MPI) and Part 3 (for the targets needed).
Sample output
$ make plot mpif90 -c random_util.f90 mpif90 -c problem_description.f90 mpif90 -c mc_walk.f90 mpif90 -c laplace_mc.f90 mpif90 random_util.o problem_description.o mc_walk.o laplace_mc.o -o test.exe mpiexec -n 4 test.exe seed1 for random number generator: 12442 seed1 for random number generator: 12539 seed1 for random number generator: 12636 seed1 for random number generator: 12345 10 0.516750000000000E+00 0.148333E+00 20 0.478500000000000E+00 0.633333E-01 40 0.425437500000000E+00 0.545833E-01 80 0.431562500000000E+00 0.409722E-01 160 0.431593750000000E+00 0.409028E-01 320 0.425703125000000E+00 0.539931E-01 640 0.426492187500000E+00 0.522396E-01 1280 0.427759765624999E+00 0.494227E-01 2560 0.430487304687498E+00 0.433615E-01 5120 0.443433105468749E+00 0.145931E-01 10240 0.449190429687505E+00 0.179905E-02 20480 0.449556518554698E+00 0.985514E-03 40960 0.451413696289083E+00 0.314155E-02 Final approximation to u(x0,y0): 4.51413696289083E-01 Total walks performed by all processes: 40960 Walks performed by Process 0: 0 Walks performed by Process 1: 12928 Walks performed by Process 2: 13414 Walks performed by Process 3: 14618 python plot_mc_laplace_error.py
Your project directory should contain:
For 583 students:
As usual, commit your results, push to bitbucket, and see the Canvas course page for the link to submit the SHA-1 hash code. These should be submitted by the due date/time to receive full credit.
Then have a good summer!