


Next: Fast Fourier Transform -
Up: Math 465, Computer Projects
Previous: Bairstow's Method - due
Write a program to compute
- 1.
- The orthogonal polynomials with respect to a discrete weighted inner
product on a data set of xi.
- 2.
- The expansion coefficients of a least squares polynomial approximation
to a given function based on these polynomials and the data values
yi=f(xi).
- 3.
- The values at a given number of equally spaced points of any
least squares polynomial based on these orthogonal polynomials.
The inputs to the overall program should be
n,w,x,y,m,d where n is the
number of data points, w is an n dimensional vector of weights,
the data points are
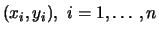 ,
m+1 is the number of
evaluation points and d is the maximum degree of the set of orthogonal
polynomials. The subprogram for (1) should generate polynomials
,
m+1 is the number of
evaluation points and d is the maximum degree of the set of orthogonal
polynomials. The subprogram for (1) should generate polynomials
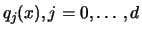 which
are orthogonal with respect to the inner product
which
are orthogonal with respect to the inner product
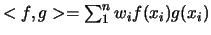 .
These polynomials should be calculated according to the
three term recurrence relation described on pages 268-270. The subprogram (2)
should compute the ``Fourier'' coefficients
ck=<y,qk>/<qk,qk> of
the ``function'' y. And the subprogram (3) should calculate
the values of the approximation
.
These polynomials should be calculated according to the
three term recurrence relation described on pages 268-270. The subprogram (2)
should compute the ``Fourier'' coefficients
ck=<y,qk>/<qk,qk> of
the ``function'' y. And the subprogram (3) should calculate
the values of the approximation
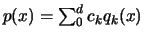 at m+1 equally spaced points in the interval [x1,xn].
at m+1 equally spaced points in the interval [x1,xn].
Run your program with the following data and plot the approximation p.
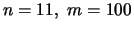 ,
,
w=(1,1,1,1,1,1,1,1,1,1,1),
x=(-5,-4,-3,-2,-1,0,1,2,3,4,5),
y=(3,2,3,5,3,4,3,2,2,3,2),
d=2,5,10, (one run for each value of d)
Also run and plot the approximations when
y=1/(1+x2).
(The d=10 case is a polynomial interpolant (Why?) and should
remind you of one of the polynomial interpolants plotted last quarter.)



Next: Fast Fourier Transform -
Up: Math 465, Computer Projects
Previous: Bairstow's Method - due
David Ragozin
1999-12-22
![]() ,
,