Pareto optimality is a concept in multi-criteria optimization that allows for the optimization of a vector of multiple criteria, enabling all tradeoffs among optimal combinations of multiple criteria to be evaluated. The figure on the top left illustrates a simple case of minimizing two criteria simultaneously (Z1, Z2), with the solid line indicating the Pareto optimal frontier (whereby any improvement with respect to Z1 comes at the expense of Z2). Each point along that frontier represents a unique model parameterization and/or model structure, so Pareto optimality identifies multiple Pareto optimal solutions. Through this procedure a scientist is able to investigate differences among the multiple optimal solutions that are able to optimize varying combinations of assessment criteria. Pareto optimality originated with the concept of efficiency in economics, and has recently been applied to various problems in ecology.
Many problems in ecology are complex and difficult to evaluate empirically, so we rely on simulation models to aid our understanding of dynamic ecosystem processes. Although a simplification of the system of interest, these models themselves are often quite complex and require sophisticated methods for their development, assessment and inference. There is no obvious choice of a single criterion to evaluate ecological models, and there are few methods that allow multiple criteria to be incorporated into the model assessment process.
Pareto optimality with binary error measures was introduced by Reynolds and Ford (1999) as a method for ecological model assessment. The basic premise is that ecological models are complex and their outputs are multivariate. In order to better evaluate whether a model is adequate for the objectives of the modelling exercise, model outputs must be compared against multiple criteria that characterize the system of interest. These criteria are quantified using target ranges, such that the model is considered to satisfy a criterion if its output falls within the target range. For example, a model of branch morphogenesis would be considered adequate if it was able to replicate the basic foliage demography (e.g., achieve the number of shoots within a range expected for a given species). However, many different branch morphologies can have the same number of shoots. The spatial distribution of foliage on that branch is also an important criterion in assessing the adequacy of the model. Any model structure able to satisfy both the number of shoots and a metric of their spatial arrangement would be considered superior to any model that can accomplish one, but not the other measure. This framework becomes more complicated as the number of criteria a model is made to satisfy increases.
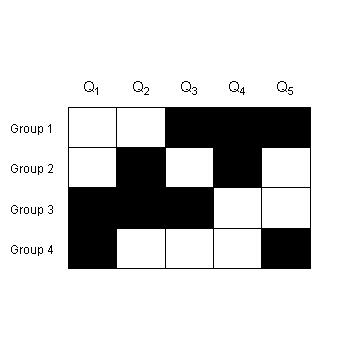
In the checkerboard figure on the top right the model is compared against 5 criteria (Q1,...,Q5). There are four groups, each able to achieve a different combination of criteria (black boxes) and no one group able to achieve all criteria simultaneously. We can compare these groups to understand the tradeoffs and limitations in model structure that enable some, but not all of the criteria to be satisfied. By increasing the demands on the model structure, we are able to uncover sources of model inadequacy. See Kennedy and Ford (2009) for a more detailed example with two binary error measures.
We recently explored the application of Pareto optimality to environmental decision-making with a case study for fire and fuels management (Kennedy et al. 2008). The motivation of this effort is to incorporate ecological values into the decision-making process and we consider Pareto optimality to be an ideal tool to enable informed decision-making in the context of the tradeoffs inherent in fuels management. Our effort focused on balancing the effects of fuels treatments on wildlife habitat with the risk of catastrophic fire on the landscape.
Pareto optimality also has great promise to advance the role of models in optimality studies for biology and ecology by providing a platform with which multiple system characteristics can be integrated to form more complete explanations of ecological phenomena. Organisms contend with multiple stresses simultaneously and they must perform many functions in order to survive and reproduce. Organisms are not inevitably optimal entities for any single function, and multiple structures can be considered equivalently optimal for a suite of functions. Optimality studies are best utilized to uncover the trade-offs that prevent organisms from achieving optimal states and to describe those multiple optimal solutions. We used Pareto optimality to uncover possible tradeoffs in the morphology of old-growth Douglas-fir branches and to explain how Douglas-fir is able to persist well beyond attaining its maximum height and crown width. See the page on old-growth branches for more details of this study.