STATIONARY STATE SKEWNESS IN KPZ TYPE GROWTH

Growth in Scale Invariance
Marcel den Nijs, 6th APCTP Bulletin, Korea (2000).

Stationary State Skewness in Two Dimensional KPZ Type Growth
Chen-Shan Chin and Marcel den Nijs, Phys. Rev. E, 59 , 2633-2641 (1999).

Stationary State Skewness in KPZ Type Growth
Marcel den Nijs and John Neergaard, J.Phys. A 30, 1935 (1997).

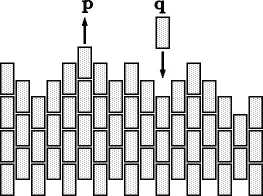BCSOS model growth rule

surface growth:

KPZ type growth represents one of the generic surface growth processes.
The surface grows by deposition and evaporation at randomly selected surface sites, with a probability that varies with the local properties of the surface configuration.
For example, at valley bottoms (hill tops) the surface growth is enhanced (suppressed), with respect to the average growth velocity. At sloped segments the growth is suppressed or enhanced (this varies with the properties of the microscopic model).
This is often modeled at the microscopic atomic level by master equation type stochastic processes.

At meso-scopic scales such processes are often modeled by Langevin equations. The bare stochastic deposition rate is modified by the local surface structure.
For example, the surface grows faster in valley bottoms and slower at hill tops, i.e., we must include a term proportional to the surface curvature in the Langevin equation. In the absence of other terms, the Langevin equation is linear (a diffusion equation with noise). Such dynamic processes are known as Edwards-Wilkinson growth.
Karder, Parisi, and Zhang (KPZ) pointed out that the slope dependence leads to a non-linear term (the square of the slope), and that such a term is generically present.
The random noise keeps the surface active and rough. In the stationary state the root-mean square of the height difference between two points along the surface grows with distance as a powerlaw r^a with a=1/2 in one dimension and a=2/5 in two dimensions.
This absence of a characteristic length scale also shows in the approach to the stationary growing state. The characteristic time scale at which the surface reaches the stationary state diverges with surface width L as, t~L^z, with dynamic critical exponent z=2-a.
These scaling properties of the surface are robust and universal and do not vary with the details of microscopic growth rule. They only change in the presence of additional conservation laws.

stationary state skewness:

Stationary states in KPZ type growth typically lack of particle-hole symmetry. The surface lacks particle-hole symmetry, and is skewed. For example, hill-tops are flatter than valley bottoms (at large resulutions), and the odd moments of the height distribution function are non-zero.
In 1D KPZ growth this skewness is non-universal and can be tuned by changing the detail of the growth rule. This is caused by the fact that the KPZ fixed point lies in 1D in the sub space of zero skewness, while a typical KPZ type process, like the Kim-Kosterlitz model, is inside that sub space.
We demonstrated using finite size scaling that the third moment of the surface width distribution diverges in 1D as function of system size with exponent 3a+y(sk) , where y(sk) = -1 is the scaling exponent of the leading particle-hole breaking skewness generating interaction. The skewness amplitude is non universal.

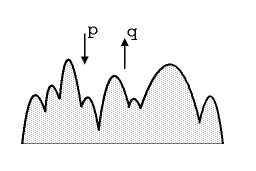In 2D, skewness is intrinsic to the scale invariance of the surface profile. It is non-tunable, and is typically negative. The third moment now scales with exponent 3a, and the amplitude ratio's of the various moments of the stationary state height distribution are universal. We established that these ratio's are indeed universal, and we determined some of their values .
In addition, we clarified a lingering issue concerning the universality of the 2D roughness exponent, a=2/5. The spread in numerical values quoted in the literature, in particular between the KK and BCSOS models can be understood in terms of strong corrections to finite size scaling.

home page of Marcel den Nijs