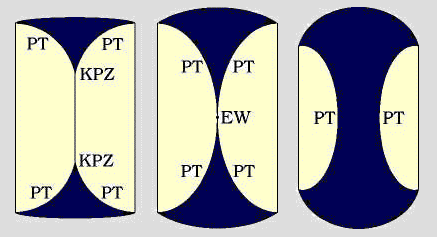
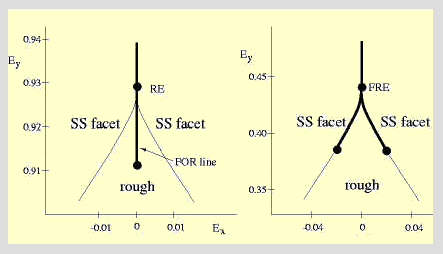
Facet-ridge end points in equilibrium crystal shapes are points where a sharp first-order boundary between two facets splits into two lines with rough rounded crystal in between.

The figure above shows a typical temperature evolution of such a crystal structure.

We found an exact mapping of the transfer matrix at the facet ridge end point in the so-called BCSOS model onto one dimensional KPZ type growth . The spatial direction parallel to the facet ridge play the role of time in the dynamic process.

This equivalence requires the transfer matrix to be stochastic at the facet-ridge end-point. This must be coincidental, and the question arises whether the scaling exponents of facet-ridge end-points are different from the KPZ values in general.

Indeed, the inclusion of more interactions leads to crystal shapes with more structure . In particular, we find first-order lines sticking into the rough rounded part of the crystal and first-order boundaries between the facets and the rounded parts .