[CS logo]

CSPP 56553 - Artificial Intelligence
Winter 2004
Homework #2: Due January 28, 2004

Goals

Through this assignment you will:

Background

In this assignment we examine the problem of finding a consistent set of assignments to a set of variables, X1, X2,...Xn, where each variable Xi takes its values from a domain Di. The assignments are restricted by a set of pairwise constraints between the variables. The constraints can be arbitrary functions, so the problems described can be quite general.

Problem 1

We begin by examining a common problem and reformulating it as a constraint satisfaction problem.

Here we will analyze a simplification of the crossword puzzle problem. In this variant, we assume that we have a set of words W1, W2,...Wn and a crossword puzzle grid. Our goal is to fill the crossword grid with the words such that letters of intersecting words match. An example of an uncompleted puzzle and a completed puzzle appear below.

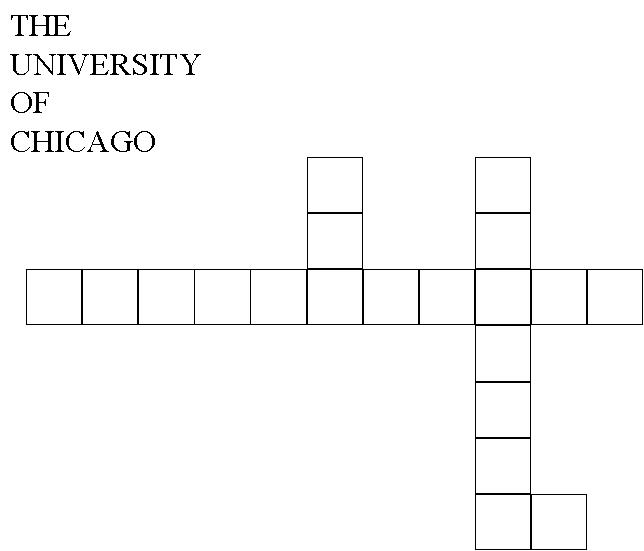
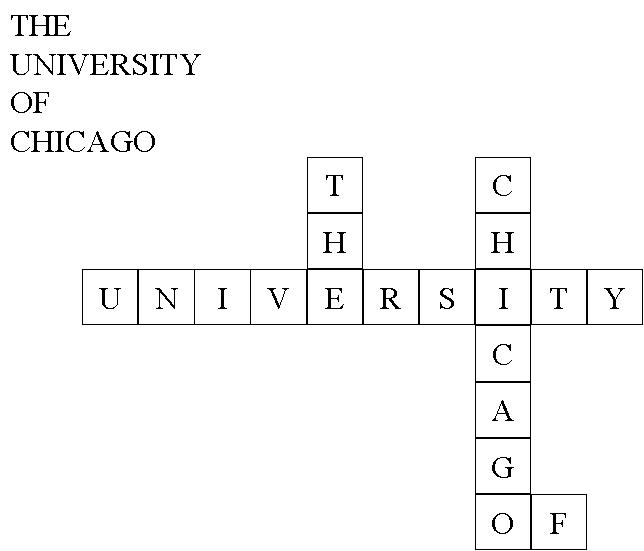
Provide a constraint satisfaction problem formulation for this variant of the crossword puzzle problem.

Part A

Specify the variables to which values are to be assigned.

Part B

Specify the domains from which the variables take their values.

Part C

Define the constraints that must hold between variables. Please provide pseudo-code defining the constraints explicitly.

Part D

Give a simple example of a "fill-in" (crossword) puzzle of the type above that demonstrates the limitations of arc-consistency type constraint propagation for solving constraint satisfaction problems.

Part E

Explain why constraint satisfaction procedures based on backtracking search are not subject to this problem.

Part F

Briefly describe the use of the iterative refinement, min-conflict strategy to solve the crossword puzzle problem.

Part G

Demonstrate the application of your procedure on a simple 4 word example puzzle.

Background 2

The remaining problems will compare the effectiveness of different strategies for solving constraint satisfaction problems such as the one defined above. We will make use of the java applet from MIT demonstrated in class that solves the map coloring problem. This applet can be found here. It requires the Java 2 plug-in, so all details required to answer the problems are included below.

Problem 2

The applet demonstrated in class uses a basic backtracking procedure as the foundation for finding solutions to the constraint satisfaction problem.

Part A

When we run the map-coloring applet with 4 colors on the map of the continental United States, we observe that when a solution is finally reached no constraints checks have been performed. Explain the mechanism that plain backtracking search needs to use to find valid labelings without constraint checks.

Part B

Conversely, backtracking with forward checking performs 492 constraint checks, and encounters 0 dead ends. Explain briefly how forward checking avoids dead ends.

Problem 3

In the discussion above, we assumed a static alphabetical ordering on nodes to search. Here we try apply some heuristics to find satisfying assignments more rapidly.

Part A

Selecting the most constrained variable to expand next in backtracking with forward checking results in a legal coloring after 299 constraint checks and 0 dead ends. In contrast, the naive alphabetic ordering required 492 constraint checks and 0 dead ends. Explain this improvement by characterizing the impact of the selection of most constrained variable on measures associated with cost of depth-first backtracking search.

Part B

Although it might seem counter-intuitive, the best choice of value assignment is often "least constraining". Explain briefly why one would choose to make the least constraining value assignment to a variable.

Background 3

Genetic algorithms build on a biological analogy as mechanism for local search and learning. The inspiration lies in Darwin's theory of evolution by natural selection. In natural evolution, individuals have traits carried by genes on chromosomes that are passed on to offspring. Variation in genetic make-up arise through mutation - copying errors - and crossover combining material from different chromosomes. The fittest individuals survive to have more offspring.

Genetic algorithms map the structure of the search problem onto evolutionary analogs. The features or parameters of the search space map to genes and are grouped into chromosomes. Mutations correspond to random changes in some number of feature values. Crossover likewise corresponds to swapping feature values for some subset of genes between a pair of chromosomes. Finally one has to define a measure of fitness. We explored the standard method, rank method, and rank-space methods of computing fitness as the probability of an individual's survival to the next generation. These measures draw on assessments of quality, diversity or both.

Problem 4: Mastermind

Mastermind is a game in which one player creates a pattern of colored pegs, which they hide from the other player. The other player's goal is to guess the hidden pattern of pegs based on limited feedback (number of correct colors, number of correctly positioned pegs). Here we will consider using GAs to evolve a solution to the mastermind matching game.

In this variant of the game, the pegs will take on the colors of the rainbow: red, orange, yellow, green, blue, indigo, violet. If we had all the processing power of a computer to solve this problem, we could try to guess a longer than typical string, 20 pegs in length, "rgybvgbiyoroggviiybo". Formulate mastermind as a GA. Specifically, specify the mapping to genes and chromosomes. Describe a quality measure. Describe a mutation operator.