For a sample of size $n$, two-sided critical values are given for significance levels .10, .05, and .01. Reject the null hypothesis of independence if the absolute value of the sample Spearman correlation coefficient exceeds the tabled value.

Table 1: Critical values for Spearman's rank correlation coefficient.

	Two-sided 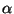$\alpha$
	.10	.05	.01
$n$
5	.900	--	--
6	.829	.886	--
7	.714	.786	.929
8	.643	.738	.881
9	.600	.700	.833
10	.564	.648	.794
11	.536	.618	.818
12	.497	.591	.780
13	.475	.566	.745
14	.457	.545	.716
15	.441	.525	.689
16	.425	.507	.666
17	.412	.490	.645
18	.399	.476	.625
19	.388	.462	.608
20	.377	.450	.591
21	.368	.438	.576
22	.359	.428	.562
23	.351	.418	.549
24	.343	.409	.537
25	.336	.400	.526
26	.329	.392	.515
27	.323	.385	.505
28	.317	.377	.496
29	.311	.370	.487
30	.305	.364	.478