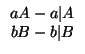Consider a 2 by 2 table: $\begin{array}{c} a A-a \vert A\\ b B-b \vert B \end{array}$ with rows and/or columns exchanged so that (1) $A\geq B$ and (2)  $(a/A)\geq (b/B)$. The table entries are ordered lexicographically by $A$ (ascending). $B$ (descending) and $a$ (descending). For each triple $(A,B,a)$ the table presents critical values for one-sided tests of the hypothesis that the true proportion corresponding to $a/A$ is greater than the true proportion corresponding to $b/B$. Significance levels of 0.05, 0.025 and 0.01 are considered. For $A\leq 15$ all values where critical values exist are tabulated. For each significance level two columns give: (1) the nominal critical value for $b$ (that is, reject the null hypothesis if the observed $b$ is less than or equal to the table entry) and (2) the $p$-value corresponding to the critical value (this is less than the nominal significance level in most cases due to the discreteness of the distribution).
Table 1: Fisher's exact test for $2 \times 2$ tables.
$A$ $B$ $a$ $b$ $p$ $b$ $p$ $b$ $p$
3 3 3 0 .050 -- -- -- --
4 4 4 0 .014 0 .014 -- --
4 3 4 0 .029 -- -- -- --
5 5 5 1 .024 1 .024 0 .004
5 5 4 0 .024 0 .024 -- --
5 4 5 1 .048 0 .008 0 .008
5 4 4 0 .040 -- -- -- --
5 3 5 0 .018 0 .018 -- --
5 2 5 0 .048 -- -- -- --
6 6 6 2 .030 1 .008 1 .008
6 6 5 1 .040 0 .008 0 .008
6 6 4 0 .030 -- -- -- --
6 5 6 1 .015 1 .015 0 .002
6 5 5 0 .013 0 .013 -- --
6 5 4 0 .045 -- -- -- --
6 4 6 1 .033 0 .005 0 .005
6 4 5 0 .024 0 .024 -- --
6 3 6 0 .012 0 .012 -- --
6 3 5 0 .048 -- -- -- --
6 2 6 0 .036 -- -- -- --
7 7 7 3 .035 2 .010 1 .002
7 7 6 1 .015 1 .015 0 .002
7 7 5 0 .010 0 .010 -- --
7 7 4 0 .035 -- -- -- --
7 6 7 2 .021 2 .021 1 .005
7 6 6 1 .025 0 .004 0 .004
7 6 5 0 .016 0 .016 -- --
7 6 4 0 .049 -- -- -- --
7 5 7 2 .045 1 .010 0 .001
7 5 6 1 .045 0 .008 0 .008
7 5 5 0 .027 -- -- -- --
7 4 7 1 .024 1 .024 0 .003
7 4 6 0 .015 0 .015 -- --
7 4 5 0 .045 -- -- -- --
7 3 7 0 .008 0 .008 0 .008
7 3 6 0 .033 -- -- -- --
7 2 7 0 .028 -- -- -- --
8 8 8 4 .038 3 .013 2 .003
8 8 7 2 .020 2 .020 1 .005
8 8 6 1 .020 1 .020 0 .003
8 8 5 0 .013 0 .013 -- --
8 8 4 0 .038 -- -- -- --
8 7 8 3 .026 2 .007 2 .007
8 7 7 2 .035 1 .009 1 .009
8 7 6 1 .032 0 .006 0 .006
8 7 5 0 .019 0 .019 -- --
8 6 8 2 .015 2 .015 1 .003
8 6 7 1 .016 1 .016 0 .002
8 6 6 0 .009 0 .009 0 .009
8 6 5 0 .028 -- -- -- --
8 5 8 2 .035 1 .007 1 .007
8 5 7 1 .032 0 .005 0 .005
8 5 6 0 .016 0 .016 -- --
8 5 5 0 .044 -- -- -- --
8 4 8 1 .018 1 .018 0 .002
8 4 7 0 .010 0 .010 -- --
8 4 6 0 .030 -- -- -- --
8 3 8 0 .006 0 .006 0 .006
8 3 7 0 .024 0 .024 -- --
8 2 8 0 .022 0 .022 -- --
9 9 9 5 .041 4 .015 3 .005
9 9 8 3 .025 3 .025 2 .008
9 9 7 2 .028 1 .008 1 .008
9 9 6 1 .025 1 .025 0 .005
9 9 5 0 .015 0 .015 -- --
9 9 4 0 .041 -- -- -- --
9 8 9 4 .029 3 .009 3 .009
9 8 8 3 .043 2 .013 1 .003
9 8 7 2 .044 1 .012 0 .002
9 8 6 1 .036 0 .007 0 .007
9 8 5 0 .020 0 .020 -- --
9 7 9 3 .019 3 .019 2 .005
9 7 8 2 .024 2 .024 1 .006
9 7 7 1 .020 1 .020 0 .003
9 7 6 0 .010 0 .010 -- --
9 7 5 0 .029 -- -- -- --
9 6 9 3 .044 2 .011 1 .002
9 6 8 2 .047 1 .011 0 .001
9 6 7 1 .035 0 .006 0 .006
9 6 6 0 .017 0 .017 -- --
9 6 5 0 .042 -- -- -- --
9 5 9 2 .027 1 .005 1 .005
9 5 8 1 .023 1 .023 0 .003
9 5 7 0 .010 0 .010 -- --
9 5 6 0 .028 -- -- -- --
9 4 9 1 .014 1 .014 0 .001
9 4 8 0 .007 0 .007 0 .007
9 4 7 0 .021 0 .021 -- --
9 4 6 0 .049 -- -- -- --
9 3 9 1 .045 0 .005 0 .005
9 3 8 0 .018 0 .018 -- --
9 3 7 0 .045 -- -- -- --
9 2 9 0 .018 0 .018 -- --
10 10 10 6 .043 5 .016 4 .005
10 10 9 4 .029 3 .010 3 .010
10 10 8 3 .035 2 .012 1 .003
10 10 7 2 .035 1 .010 1 .010
10 10 6 1 .029 0 .005 0 .005
10 10 5 0 .016 0 .016 -- --
10 10 4 0 .043 -- -- -- --
10 9 10 5 .033 4 .011 3 .003
10 9 9 4 .050 3 .017 2 .005
10 9 8 2 .019 2 .019 1 .004
10 9 7 1 .015 1 .015 0 .002
10 9 6 1 .040 0 .008 0 .008
10 9 5 0 .022 0 .022 -- --
10 8 10 4 .023 4 .023 3 .007
10 8 9 3 .032 2 .009 2 .009
10 8 8 2 .031 1 .008 1 .008
10 8 7 1 .023 1 .023 0 .004
10 8 6 0 .011 0 .011 -- --
10 8 5 0 .029 -- -- -- --
10 7 10 3 .015 3 .015 2 .003
10 7 9 2 .018 2 .018 1 .004
10 7 8 1 .013 1 .013 0 .002
10 7 7 1 .036 0 .006 0 .006
10 7 6 0 .017 0 .017 -- --
10 7 5 0 .041 -- -- -- --
10 6 10 3 .036 2 .008 2 .008
10 6 9 2 .036 1 .008 1 .008
10 6 8 1 .024 1 .024 0 .003
10 6 7 0 .010 0 .010 -- --
10 6 6 0 .026 -- -- -- --
10 5 10 2 .022 2 .022 1 .004
10 5 9 1 .017 1 .017 0 .002
10 5 8 1 .047 0 .007 0 .007
10 5 7 0 .019 0 .019 -- --
10 5 6 0 .042 -- -- -- --
10 4 10 1 .011 1 .011 0 .001
10 4 9 1 .041 0 .005 0 .005
10 4 8 0 .015 0 .015 -- --
10 4 7 0 .035 -- -- -- --
10 3 10 1 .038 0 .003 0 .003
10 3 9 0 .014 0 .014 -- --
10 3 8 0 .035 -- -- -- --
10 2 10 0 .015 0 .015 -- --
10 2 9 0 .045 -- -- -- --
11 11 11 7 .045 6 .018 5 .006
11 11 10 5 .032 4 .012 3 .004
11 11 9 4 .040 3 .015 2 .004
11 11 8 3 .043 2 .015 1 .004
11 11 7 2 .040 1 .012 0 .002
11 11 6 1 .032 0 .006 0 .006
11 11 5 0 .018 0 .018 -- --
11 11 4 0 .045 -- -- -- --
11 10 11 6 .035 5 .012 4 .004
11 10 10 4 .021 4 .021 3 .007
11 10 9 3 .024 3 .024 2 .007
11 10 8 2 .023 2 .023 1 .006
11 10 7 1 .017 1 .017 0 .003
11 10 6 1 .043 0 .009 0 .009
11 10 5 0 .023 0 .023 -- --
11 9 11 5 .026 4 .008 4 .008
11 9 10 4 .038 3 .012 2 .003
11 9 9 3 .040 2 .012 1 .003
11 9 8 2 .035 1 .009 1 .009
11 9 7 1 .025 1 .025 0 .004
11 9 6 0 .012 0 .012 -- --
11 9 5 0 .030 -- -- -- --
11 8 11 4 .018 4 .018 3 .005
11 8 10 3 .024 3 .024 2 .006
11 8 9 2 .022 2 .022 1 .005
11 8 8 1 .015 1 .015 0 .002
11 8 7 1 .037 0 .007 0 .007
11 8 6 0 .017 0 .017 -- --
11 8 5 0 .040 -- -- -- --
11 7 11 4 .043 3 .011 2 .002
11 7 10 3 .047 2 .013 1 .002
11 7 9 2 .039 1 .009 1 .009
11 7 8 1 .025 1 .025 0 .004
11 7 7 0 .010 0 .010 -- --
11 7 6 0 .025 0 .025 -- --
11 6 11 3 .029 2 .006 2 .006
11 6 10 2 .028 1 .005 1 .005
11 6 9 1 .018 1 .018 0 .002
11 6 8 1 .043 0 .007 0 .007
11 6 7 0 .017 0 .017 -- --
11 6 6 0 .037 -- -- -- --
11 5 11 2 .018 2 .018 1 .003
11 5 10 1 .013 1 .013 0 .001
11 5 9 1 .036 0 .005 0 .005
11 5 8 0 .013 0 .013 -- --
11 5 7 0 .029 -- -- -- --
11 4 11 1 .009 1 .009 1 .009
11 4 10 1 .033 0 .004 0 .004
11 4 9 0 .011 0 .011 -- --
11 4 8 0 .026 -- -- -- --
11 3 11 1 .033 0 .003 0 .003
11 3 10 0 .011 0 .011 -- --
11 3 9 0 .027 -- -- -- --
11 2 11 0 .013 0 .013 -- --
11 2 10 0 .038 -- -- -- --
12 12 12 8 .047 7 .019 6 .007
12 12 11 6 .034 5 .014 4 .005
12 12 10 5 .045 4 .018 3 .006
12 12 9 4 .050 3 .020 2 .006
12 12 8 3 .050 2 .018 1 .005
12 12 7 2 .045 1 .014 0 .002
12 12 6 1 .034 0 .007 0 .007
12 12 5 0 .019 0 .019 -- --
12 12 4 0 .047 -- -- -- --
12 11 12 7 .037 6 .014 5 .005
12 11 11 5 .024 5 .024 4 .008
12 11 10 4 .029 3 .010 2 .003
12 11 9 3 .030 2 .009 2 .009
12 11 8 2 .026 1 .007 1 .007
12 11 7 1 .019 1 .019 0 .003
12 11 6 1 .045 0 .009 0 .009
12 11 5 0 .024 0 .024 -- --
12 10 12 6 .029 5 .010 5 .010
12 10 11 5 .043 4 .015 3 .005
12 10 10 4 .048 3 .017 2 .005
12 10 9 3 .046 2 .015 1 .004
12 10 8 2 .038 1 .010 0 .002
12 10 7 1 .026 0 .005 0 .005
12 10 6 0 .012 0 .012 -- --
12 10 5 0 .030 -- -- -- --
12 9 12 5 .021 5 .021 4 .006
12 9 11 4 .029 3 .009 3 .009
12 9 10 3 .029 2 .008 2 .008
12 9 9 2 .024 2 .024 1 .006
12 9 8 1 .016 1 .016 0 .002
12 9 7 1 .037 0 .007 0 .007
12 9 6 0 .017 0 .017 -- --
12 9 5 0 .039 -- -- -- --
12 8 12 5 .049 4 .014 3 .004
12 8 11 3 .018 3 .018 2 .004
12 8 10 2 .015 2 .015 1 .003
12 8 9 2 .040 1 .010 1 .010
12 8 8 1 .025 1 .025 0 .004
12 8 7 0 .010 0 .010 -- --
12 8 6 0 .024 0 .024 -- --
12 7 12 4 .036 3 .009 3 .009
12 7 11 3 .038 2 .010 2 .010
12 7 10 2 .029 1 .006 1 .006
12 7 9 1 .017 1 .017 0 .002
12 7 8 1 .040 0 .007 0 .007
12 7 7 0 .016 0 .016 -- --
12 7 6 0 .034 -- -- -- --
12 6 12 3 .025 3 .025 2 .005
12 6 11 2 .022 2 .022 1 .004
12 6 10 1 .013 1 .013 0 .002
12 6 9 1 .032 0 .005 0 .005
12 6 8 0 .011 0 .011 -- --
12 6 7 0 .025 0 .025 -- --
12 6 6 0 .050 -- -- -- --
12 5 12 2 .015 2 .015 1 .002
12 5 11 1 .010 1 .010 1 .010
12 5 10 1 .028 0 .003 0 .003
12 5 9 0 .009 0 .009 0 .009
12 5 8 0 .020 0 .020 -- --
12 5 7 0 .041 -- -- -- --
12 4 12 2 .050 1 .007 1 .007
12 4 11 1 .027 0 .003 0 .003
12 4 10 0 .008 0 .008 0 .008
12 4 9 0 .019 0 .019 -- --
12 4 8 0 .038 -- -- -- --
12 3 12 1 .029 0 .002 0 .002
12 3 11 0 .009 0 .009 0 .009
12 3 10 0 .022 0 .022 -- --
12 3 9 0 .044 -- -- -- --
12 2 12 0 .011 0 .011 -- --
12 2 11 0 .033 -- -- -- --
13 13 13 9 .048 8 .020 7 .007
13 13 12 7 .037 6 .015 5 .006
13 13 11 6 .048 5 .021 4 .008
13 13 10 4 .024 4 .024 3 .008
13 13 9 3 .024 3 .024 2 .008
13 13 8 2 .021 2 .021 1 .006
13 13 7 2 .048 1 .015 0 .003
13 13 6 1 .037 0 .007 0 .007
13 13 5 0 .020 0 .020 -- --
13 13 4 0 .048 -- -- -- --
13 12 13 8 .039 7 .015 6 .005
13 12 12 6 .027 5 .010 5 .010
13 12 11 5 .033 4 .013 3 .004
13 12 10 4 .036 3 .013 2 .004
13 12 9 3 .034 2 .011 1 .003
13 12 8 2 .029 1 .008 1 .008
13 12 7 1 .020 1 .020 0 .004
13 12 6 1 .046 0 .010 0 .010
13 12 5 0 .024 0 .024 -- --
13 11 13 7 .031 6 .011 5 .003
13 11 12 6 .048 5 .018 4 .006
13 11 11 4 .021 4 .021 3 .007
13 11 10 3 .021 3 .021 2 .006
13 11 9 3 .050 2 .017 1 .004
13 11 8 2 .040 1 .011 0 .002
13 11 7 1 .027 0 .005 0 .005
13 11 6 0 .013 0 .013 -- --
13 11 5 0 .030 -- -- -- --
13 10 13 6 .024 6 .024 5 .007
13 10 12 5 .035 4 .012 3 .003
13 10 11 4 .037 3 .012 2 .003
13 10 10 3 .033 2 .010 1 .002
13 10 9 2 .026 1 .006 1 .006
13 10 8 1 .017 1 .017 0 .003
13 10 7 1 .038 0 .007 0 .007
13 10 6 0 .017 0 .017 -- --
13 10 5 0 .038 -- -- -- --
13 9 13 5 .017 5 .017 4 .005
13 9 12 4 .023 4 .023 3 .007
13 9 11 3 .022 3 .022 2 .006
13 9 10 2 .017 2 .017 1 .004
13 9 9 2 .040 1 .010 0 .001
13 9 8 1 .025 1 .025 0 .004
13 9 7 0 .010 0 .010 -- --
13 9 6 0 .023 0 .023 -- --
13 9 5 0 .049 -- -- -- --
13 8 13 5 .042 4 .012 3 .003
13 8 12 4 .047 3 .014 2 .003
13 8 11 3 .041 2 .011 1 .002
13 8 10 2 .029 1 .007 1 .007
13 8 9 1 .017 1 .017 0 .002
13 8 8 1 .037 0 .006 0 .006
13 8 7 0 .015 0 .015 -- --
13 8 6 0 .032 -- -- -- --
13 7 13 4 .031 3 .007 3 .007
13 7 12 3 .031 2 .007 2 .007
13 7 11 2 .022 2 .022 1 .004
13 7 10 1 .012 1 .012 0 .002
13 7 9 1 .029 0 .004 0 .004
13 7 8 0 .010 0 .010 -- --
13 7 7 0 .022 0 .022 -- --
13 7 6 0 .044 -- -- -- --
13 6 13 3 .021 3 .021 2 .004
13 6 12 2 .017 2 .017 1 .003
13 6 11 2 .046 1 .010 1 .010
13 6 10 1 .024 1 .024 0 .003
13 6 9 1 .050 0 .008 0 .008
13 6 8 0 .017 0 .017 -- --
13 6 7 0 .034 -- -- -- --
13 5 13 2 .012 2 .012 1 .002
13 5 12 2 .044 1 .008 1 .008
13 5 11 1 .022 1 .022 0 .002
13 5 10 1 .047 0 .007 0 .007
13 5 9 0 .015 0 .015 -- --
13 5 8 0 .029 -- -- -- --
13 4 13 2 .044 1 .006 1 .006
13 4 12 1 .022 1 .022 0 .002
13 4 11 0 .006 0 .006 0 .006
13 4 10 0 .015 0 .015 -- --
13 4 9 0 .029 -- -- -- --
13 3 13 1 .025 1 .025 0 .002
13 3 12 0 .007 0 .007 0 .007
13 3 11 0 .018 0 .018 -- --
13 3 10 0 .036 -- -- -- --
13 2 13 0 .010 0 .010 0 .010
13 2 12 0 .029 -- -- -- --
14 14 14 10 .049 9 .020 8 .008
14 14 13 8 .038 7 .016 6 .006
14 14 12 6 .023 6 .023 5 .009
14 14 11 5 .027 4 .011 3 .004
14 14 10 4 .028 3 .011 2 .003
14 14 9 3 .027 2 .009 2 .009
14 14 8 2 .023 2 .023 1 .006
14 14 7 1 .016 1 .016 0 .003
14 14 6 1 .038 0 .008 0 .008
14 14 5 0 .020 0 .020 -- --
14 14 4 0 .049 -- -- -- --
14 13 14 9 .041 8 .016 7 .006
14 13 13 7 .029 6 .011 5 .004
14 13 12 6 .037 5 .015 4 .005
14 13 11 5 .041 4 .017 3 .006
14 13 10 4 .041 3 .016 2 .005
14 13 9 3 .038 2 .013 1 .003
14 13 8 2 .031 1 .009 1 .009
14 13 7 1 .021 1 .021 0 .004
14 13 6 1 .048 0 .010 -- --
14 13 5 0 .025 0 .025 -- --
14 12 14 8 .033 7 .012 6 .004
14 12 13 6 .021 6 .021 5 .007
14 12 12 5 .025 4 .009 4 .009
14 12 11 4 .026 3 .009 3 .009
14 12 10 3 .024 3 .024 2 .007
14 12 9 2 .019 2 .019 1 .005
14 12 8 2 .042 1 .012 0 .002
14 12 7 1 .028 0 .005 0 .005
14 12 6 0 .013 0 .013 -- --
14 12 5 0 .030 -- -- -- --
14 11 14 7 .026 6 .009 6 .009
14 11 13 6 .039 5 .014 4 .004
14 11 12 5 .043 4 .016 3 .005
14 11 11 4 .042 3 .015 2 .004
14 11 10 3 .036 2 .011 1 .003
14 11 9 2 .027 1 .007 1 .007
14 11 8 1 .017 1 .017 0 .003
14 11 7 1 .038 0 .007 0 .007
14 11 6 0 .017 0 .017 -- --
14 11 5 0 .038 -- -- -- --
14 10 14 6 .020 6 .020 5 .006
14 10 13 5 .028 4 .009 4 .009
14 10 12 4 .028 3 .009 3 .009
14 10 11 3 .024 3 .024 2 .007
14 10 10 2 .018 2 .018 1 .004
14 10 9 2 .040 1 .011 0 .002
14 10 8 1 .024 1 .024 0 .004
14 10 7 0 .010 0 .010 0 .010
14 10 6 0 .022 0 .022 -- --
14 10 5 0 .047 -- -- -- --
14 9 14 6 .047 5 .014 4 .004
14 9 13 4 .018 4 .018 3 .005
14 9 12 3 .017 3 .017 2 .004
14 9 11 3 .042 2 .012 1 .002
14 9 10 2 .029 1 .007 1 .007
14 9 9 1 .017 1 .017 0 .002
14 9 8 1 .036 0 .006 0 .006
14 9 7 0 .014 0 .014 -- --
14 9 6 0 .030 -- -- -- --
14 8 14 5 .036 4 .010 4 .010
14 8 13 4 .039 3 .011 2 .002
14 8 12 3 .032 2 .008 2 .008
14 8 11 2 .022 2 .022 1 .005
14 8 10 2 .048 1 .012 0 .002
14 8 9 1 .026 0 .004 0 .004
14 8 8 0 .009 0 .009 0 .009
14 8 7 0 .020 0 .020 -- --
14 8 6 0 .040 -- -- -- --
14 7 14 4 .026 3 .006 3 .006
14 7 13 3 .025 2 .006 2 .006
14 7 12 2 .017 2 .017 1 .003
14 7 11 2 .041 1 .009 1 .009
14 7 10 1 .021 1 .021 0 .003
14 7 9 1 .043 0 .007 0 .007
14 7 8 0 .015 0 .015 -- --
14 7 7 0 .030 -- -- -- --
14 6 14 3 .018 3 .018 2 .003
14 6 13 2 .014 2 .014 1 .002
14 6 12 2 .037 1 .007 1 .007
14 6 11 1 .018 1 .018 0 .002
14 6 10 1 .038 0 .005 0 .005
14 6 9 0 .012 0 .012 -- --
14 6 8 0 .024 0 .024 -- --
14 6 7 0 .044 -- -- -- --
14 5 14 2 .010 2 .010 1 .001
14 5 13 2 .037 1 .006 1 .006
14 5 12 1 .017 1 .017 0 .002
14 5 11 1 .038 0 .005 0 .005
14 5 10 0 .011 0 .011 -- --
14 5 9 0 .022 0 .022 -- --
14 5 8 0 .040 -- -- -- --
14 4 14 2 .039 1 .005 1 .005
14 4 13 1 .019 1 .019 0 .002
14 4 12 1 .044 0 .005 0 .005
14 4 11 0 .011 0 .011 -- --
14 4 10 0 .023 0 .023 -- --
14 4 9 0 .041 -- -- -- --
14 3 14 1 .022 1 .022 0 .001
14 3 13 0 .006 0 .006 0 .006
14 3 12 0 .015 0 .015 -- --
14 3 11 0 .029 -- -- -- --
14 2 14 0 .008 0 .008 0 .008
14 2 13 0 .025 0 .025 -- --
14 2 12 0 .050 -- -- -- --
15 15 15 11 .050 10 .021 9 .008
15 15 14 9 .040 8 .018 7 .007
15 15 13 7 .025 6 .010 5 .004
15 15 12 6 .030 5 .013 4 .005
15 15 11 5 .033 4 .013 3 .005
15 15 10 4 .033 3 .013 2 .004
15 15 9 3 .030 2 .010 1 .003
15 15 8 2 .025 1 .007 1 .007
15 15 7 1 .018 1 .018 0 .003
15 15 6 1 .040 0 .008 0 .008
15 15 5 0 .021 0 .021 -- --
15 15 4 0 .050 -- -- -- --
15 14 15 10 .042 9 .017 8 .006
15 14 14 8 .031 7 .013 6 .005
15 14 13 7 .041 6 .017 5 .007
15 14 12 6 .046 5 .020 4 .007
15 14 11 5 .048 4 .020 3 .007
15 14 10 4 .046 3 .018 2 .006
15 14 9 3 .041 2 .014 1 .004
15 14 8 2 .033 1 .009 1 .009
15 14 7 1 .022 1 .022 0 .004
15 14 6 1 .049 0 .011 -- --
15 14 5 0 .025 -- -- -- --
15 13 15 9 .035 8 .013 7 .005
15 13 14 7 .023 7 .023 6 .009
15 13 13 6 .029 5 .011 4 .004
15 13 12 5 .031 4 .012 3 .004
15 13 11 4 .030 3 .011 2 .003
15 13 10 3 .026 2 .008 2 .008
15 13 9 2 .020 2 .020 1 .005
15 13 8 2 .043 1 .013 0 .002
15 13 7 1 .029 0 .005 0 .005
15 13 6 0 .013 0 .013 -- --
15 13 5 0 .031 -- -- -- --
15 12 15 8 .028 7 .010 7 .010
15 12 14 7 .043 6 .016 5 .006
15 12 13 6 .049 5 .019 4 .007
15 12 12 5 .049 4 .019 3 .006
15 12 11 4 .045 3 .017 2 .005
15 12 10 3 .038 2 .012 1 .003
15 12 9 2 .028 1 .007 1 .007
15 12 8 1 .018 1 .018 0 .003
15 12 7 1 .038 0 .007 0 .007
15 12 6 0 .017 0 .017 -- --
15 12 5 0 .037 -- -- -- --
15 11 15 7 .022 7 .022 6 .007
15 11 14 6 .032 5 .011 4 .003
15 11 13 5 .034 4 .012 3 .003
15 11 12 4 .032 3 .010 2 .003
15 11 11 3 .026 2 .008 2 .008
15 11 10 2 .019 2 .019 1 .004
15 11 9 2 .040 1 .011 0 .002
15 11 8 1 .024 1 .024 0 .004
15 11 7 1 .049 0 .010 0 .010
15 11 6 0 .022 0 .022 -- --
15 11 5 0 .046 -- -- -- --
15 10 15 6 .017 6 .017 5 .005
15 10 14 5 .023 5 .023 4 .007
15 10 13 4 .022 4 .022 3 .007
15 10 12 3 .018 3 .018 2 .005
15 10 11 3 .042 2 .013 1 .003
15 10 10 2 .029 1 .007 1 .007
15 10 9 1 .016 1 .016 0 .002
15 10 8 1 .034 0 .006 0 .006
15 10 7 0 .013 0 .013 -- --
15 10 6 0 .028 -- -- -- --
15 9 15 6 .042 5 .012 4 .003
15 9 14 5 .047 4 .015 3 .004
15 9 13 4 .042 3 .013 2 .003
15 9 12 3 .032 2 .009 2 .009
15 9 11 2 .021 2 .021 1 .005
15 9 10 2 .045 1 .011 0 .002
15 9 9 1 .024 1 .024 0 .004
15 9 8 1 .048 0 .009 0 .009
15 9 7 0 .019 0 .019 -- --
15 9 6 0 .037 -- -- -- --
15 8 15 5 .032 4 .008 4 .008
15 8 14 4 .033 3 .009 3 .009
15 8 13 3 .026 2 .006 2 .006
15 8 12 2 .017 2 .017 1 .003
15 8 11 2 .037 1 .008 1 .008
15 8 10 1 .019 1 .019 0 .003
15 8 9 1 .038 0 .006 0 .006
15 8 8 0 .013 0 .013 -- --
15 8 7 0 .026 -- -- -- --
15 8 6 0 .050 -- -- -- --
15 7 15 4 .023 4 .023 3 .005
15 7 14 3 .021 3 .021 2 .004
15 7 13 2 .014 2 .014 1 .002
15 7 12 2 .032 1 .007 1 .007
15 7 11 1 .015 1 .015 0 .002
15 7 10 1 .032 0 .005 0 .005
15 7 9 0 .010 0 .010 -- --
15 7 8 0 .020 0 .020 -- --
15 7 7 0 .038 -- -- -- --
15 6 15 3 .015 3 .015 2 .003
15 6 14 2 .011 2 .011 1 .002
15 6 13 2 .031 1 .006 1 .006
15 6 12 1 .014 1 .014 0 .002
15 6 11 1 .029 0 .004 0 .004
15 6 10 0 .009 0 .009 0 .009
15 6 9 0 .017 0 .017 -- --
15 6 8 0 .032 -- -- -- --
15 5 15 2 .009 2 .009 2 .009
15 5 14 2 .032 1 .005 1 .005
15 5 13 1 .014 1 .014 0 .001
15 5 12 1 .031 0 .004 0 .004
15 5 11 0 .008 0 .008 0 .008
15 5 10 0 .016 0 .016 -- --
15 5 9 0 .030 -- -- -- --
15 4 15 2 .035 1 .004 1 .004
15 4 14 1 .016 1 .016 0 .001
15 4 13 1 .037 0 .004 0 .004
15 4 12 0 .009 0 .009 0 .009
15 4 11 0 .018 0 .018 -- --
15 4 10 0 .033 -- -- -- --
15 3 15 1 .020 1 .020 0 .001
15 3 14 0 .005 0 .005 0 .005
15 3 13 0 .012 0 .012 -- --
15 3 12 0 .025 0 .025 -- --
15 3 11 0 .043 -- -- -- --
15 2 15 0 .007 0 .007 0 .007
15 2 14 0 .022 0 .022 -- --
15 2 13 0 .044 -- -- -- --
23 10 21 5 .016 5 .016 4 .004
32 13 32 10 .020 10 .020 9 .005


Let $P_{A}$ and $P_{B}$ be the true proportions in two populations. The sample size, $N$, for two equally sized groups is tabulated for one-sided significance level $\alpha$ and probability $\beta$ of not rejecting the null hypothesis. Each rectangular portion of the table contains sample sizes for two pairs of $\alpha$ and $\beta$ values, one above the diagonal and one below it. The arcsine approximation was used to estimate $N$.
Table 2: Sample sizes for comparing two proportions with a one-sided Fisher's exact test in $2 \times 2$ tables.
$P_{A}$ $P_{B}$         $\alpha = .01$ and $\beta = .01$
  .001 .01 .05 .10 .15 .20 .25 .30 .40 .50 .60 .70 .80 .90
.001 -- 2305 288 129 81 58 45 37 26 20 15 12 10 8
.01 1679 -- 689 221 123 82 61 48 32 24 18 14 11 9
.05 210 502 -- 1169 366 191 122 87 52 35 25 19 14 11
.10 94 161 852 -- 1877 538 266 163 83 51 34 25 18 13
.15 59 90 266 1368 -- 2489 683 327 132 73 46 31 22 15
.20 43 60 140 392 1814 -- 3012 805 222 105 61 39 27 18
.25 33 44 89 194 498 2194 -- 3447 417 158 83 50 32 21
.30 27 35 63 119 239 587 2511 -- 981 256 116 64 39 25
.40 19 24 38 60 96 162 304 715 -- 1068 267 116 61 34
.50 14 17 26 37 53 77 116 187 778 -- 1068 256 105 51
.60 11 13 19 25 34 45 61 84 195 778 -- 981 222 83
.70 9 10 14 18 23 29 37 47 84 187 715 -- 805 163
.80 7 8 11 13 16 20 24 29 45 77 162 587 -- 538
.90 6 6 8 10 11 13 15 18 25 37 60 119 392 --
            $\alpha = .01$ and $\beta = .05$ (or $\alpha = .05$ and $\beta = .01)$
$P_{A}$ $P_{B}$       $\alpha = .025$ and $\beta = .05$ (or $\alpha = .05$ and $\beta = .025)$  
  .001 .01 .05 .10 .15 .20 .25 .30 .40 .50 .60 .70 .80 .90
.001 -- 1384 173 78 49 35 27 22 16 12 9 8 6 5
.01 1119 -- 414 133 74 50 37 29 20 14 11 9 7 5
.05 140 335 -- 702 220 115 74 52 31 21 15 12 9 7
.10 63 108 568 -- 1127 323 160 98 50 31 21 15 11 8
.15 40 60 178 911 -- 1494 410 197 79 44 28 19 13 9
.20 29 40 93 261 1208 -- 1808 483 133 63 37 24 16 11
.25 22 30 60 129 332 1462 -- 2069 251 95 50 30 20 13
.30 18 23 42 79 159 391 1673 -- 589 154 70 39 24 15
.40 13 16 25 40 64 108 203 476 -- 641 161 70 37 21
.50 10 12 17 25 35 51 77 125 519 -- 641 154 63 31
.60 8 9 13 17 23 30 40 56 130 519 -- 589 133 50
.70 6 7 9 12 15 19 25 32 56 125 476 -- 483 98
.80 5 6 7 9 11 13 16 19 30 51 108 391 -- 323
.90 4 4 6 7 8 9 10 12 17 25 40 79 261 --
          $\alpha = .025$ and $\beta = .10$ (or $\alpha = .10$ and $\beta = .025)$  
$P_{A}$ $P_{B}$         $\alpha = .05$ and $\beta = .05$
  .001 .01 .05 .10 .15 .20 .25 .30 .40 .50 .60 .70 .80 .90
.001 -- 1152 144 65 41 29 23 19 13 10 8 6 5 4
.01 912 -- 345 111 62 41 31 24 16 12 9 7 6 5
.05 114 273 -- 585 183 96 61 44 26 18 13 10 7 6
.10 51 88 463 -- 939 269 133 82 42 26 17 13 9 7
.15 32 49 145 743 -- 1245 342 164 66 36 23 16 11 8
.20 23 33 76 213 985 -- 1506 403 111 53 31 20 14 9
.25 18 24 49 106 271 1192 -- 1723 209 79 42 25 16 11
.30 15 19 35 65 130 319 1364 -- 491 128 58 32 20 13
.40 11 13 21 33 52 88 165 388 -- 534 134 58 31 17
.50 8 10 14 20 29 42 63 102 423 -- 534 128 53 26
.60 6 7 10 14 18 24 33 46 106 423 -- 491 111 42
.70 5 6 8 10 13 16 20 26 46 102 388 -- 403 82
.80 4 5 6 7 9 11 13 16 24 42 88 319 -- 269
.90 3 4 5 5 6 7 9 10 14 20 33 65 213 --
          $\alpha = .05$ and $\beta = .10$ (or $\alpha = .10$ and $\beta = .05)$  
$P_{A}$ $P_{B}$         $\alpha = .10$ and $\beta = .10$
  .001 .01 .05 .10 .15 .20 .25 .30 .40 .50 .60 .70 .80 .90
.001 -- 700 88 40 25 18 14 11 8 6 5 4 3 3
.01 480 -- 210 67 38 25 19 15 10 7 6 5 4 3
.05 60 144 -- 355 111 58 37 27 16 11 8 6 5 4
.10 27 46 244 -- 570 164 81 50 25 16 11 8 6 4
.15 17 26 77 391 -- 756 208 100 40 22 14 10 7 5
.20 13 18 40 112 519 -- 914 245 68 32 19 12 8 6
.25 10 13 26 56 143 628 -- 1046 127 48 25 16 10 7
.30 8 10 18 34 69 168 718 -- 298 78 35 20 12 8
.40 6 7 11 18 28 47 87 205 -- 325 82 35 19 11
.50 4 5 8 11 15 22 33 54 223 -- 325 78 32 16
.60 4 4 6 8 10 13 18 25 56 223 -- 298 68 25
.70 3 3 4 6 7 9 11 14 25 54 205 -- 245 50
.80 2 3 3 4 5 6 7 9 13 22 47 168 -- 164
.90 2 2 3 3 4 4 5 6 8 11 18 34 112 --
          $\alpha = .10$ and $\beta = .20$ (or $\alpha = .20$ and $\beta = .10)$