MAVRIC BRAIN - Software Architecture

Neural network engine

The current version (1.0) of the neural engine for MAVRIC is called `realbrain'.  This version uses graded signals rather than pulsed action potentials.  The graded signal represesents the percent of maximum frequency (number of action potentials that could be propagated per unit time).  In this case we assume a maximum 255 pulses per second to correspond with the use of 8-bit A/D conversion in the sensory systems.  The signal is sampled every 1/10th second (micro-task cycle time for Saphira).  Thus each 100 msec a number between 0.0 and 1.0 represents an average firing rate for the interval.  Time averaging has been implemented in order to conserve on processing time given the strict time constraints in Saphira and the limitations of the present hardware.  Part of the research now involves investigation of the efficacy of this approach as compared with the pulse-coded (standard) version of adaptrode-based neurons.

This document covers the architecture of the actual brain for MAVRIC.  It does not cover the general software architecture external to the brain.  This architecture is covered under a companion document - MAVRIC General Software Architecture.

Schematic

Figure 1.  Schematic representation of objects and their relationships in an artificial brain.

The central element of an artificial brain is the array of neurons.  In the schematic (figure 1) one neuron is represented in some detail.  This schematic shows the logical relationships between elements in the brain.  In general the types of neurons and adaptrodes are stored in arrays (ntypes and atypes respectively).  Each neuron contains a pointer (black arrow) to an ntype element in the ntypes array.  Similarly, each adaptrode contains a pointer (black arrows) to an atype element in the atypes array.  These elements contain the rate constants and baseline values that are used to particularize the types of neurons and adaptrodes.

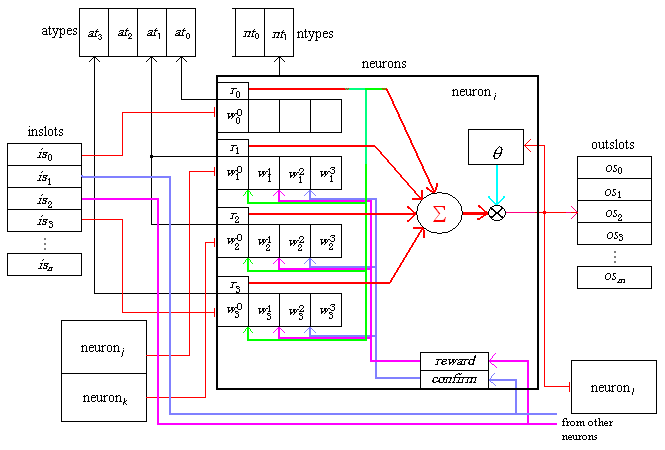
Data flows through the brain from input slots (inslots) through neurons and eventually to output slots (outslots).  The former slots' greyscale values are set by sensor and other external (body function) tasks. The latter slots provide greyscale output from neurons, usually motor outputs.  These values are used by various external (body function) tasks.

Inside a typical neuron will be an array (dynamic) of adaptrodes.  In this schematic the first adaptrode in the array (index = 0) is a non-learning unit and therefore does not employ w[1], w[2] or w[3] (shown as empty boxes).  The output from the response unit of an adaptrode (shown in red) is routed to the integrator (circle with an uppercase sigma).  In this neuron the output of the zeroth adaptrode is also used to hurdle the level 1 gate on the learning adaptrodes (green arrows).

The integrator computes a shunted summation of all of the adaptrodes (see algorithm below) which is compared with a threshold (lowercase theta).  If the sum exceeds the threshold the neuron will output a value equal to the sum.  Otherwise it will output a value equal to the exponentially decayed old output.

In some types of neurons it is useful to use dynamic thresholds, that is thresholds which can increase or decrease in value based on the activity of some other process.  Generally this will be the output activity of the neuron itself.  There are some kinds of neurons which become more resistant to stimulation, that is, the threshold rises as a function of the output of the neuron.  Other types of neurons become more excitable as a function of their own output (bursters).  Either of these types can be implemented using the output of the neuron as an up or down modulator source (red line from neuron output to the threshold box).

Learning adaptrodes get evaluative feedback from sources, generally outside the neuron.  Each neuron is assumed to have these feedback signals supplied from either input slots or from other neurons.  In a typical neuron one can find reward (purple) and confirmation (blue) feedback sources which are routed to the level 2 and level 3 potentiation gates, respectively.

Processing Algorithm

The overall algorithm for processing the `brain' of MAVRIC is as follows:

every 1/10 second
task: processBrain()
  for each inslot[i] in brain do
    compute new real inslot[i].value from inslot[i].greyscale     // 0 - 255
  for each neuron in brain do
    neuron.out_old = neuron.out_new     // prepare for next processing cycle
  for each neuron in brain do
    neuron.sum = 0               // initialize summation
    for each adaptrode in neuron do
      for each weight_vector[i], 0 <= i < 4, in adaptrode.weight_vector do
        wt[i] = weight_vector[i]        // save last values locally
      for each hurdle[i], 0 <= i < 4, in hurdle do  // also save locally
        hurdle[i].value = hurdle_source[i].value  // get gating values from hurdle sources

      adaptrode.input = adaptrode.source.output   // source is either an inslot or neuron

      compute response based on prior weight_vector[0]; if current input > MINSIGNAL
        then adaptrode.response = adaptrode.weight_vector[0],
        else adaptrode.response is exponentially decayed

      determine conditions for first-level potentiation; has input signal arrived
        before first-level hurdle? if so, set a switch (learn = 1) to allow potentiation

      determine conditions for extinction; has primary signal (input) been active but
        first-level hurdle (US signal) has not arrived in time? if so, set extinction
        flag

      // compute new weight_vector[0]
      // for notation compactness let adaptrode.weight_vector = w[]
      if extinction then
        // exponentially decay w[0] at higher rate but not below w[1]
        w[0]_new = max(w[0]_old - extinction_decay_rate * w[0]_old, w[1]_old)
      else
        w[0]_new = w[0]_old + learn * input * alpha[0] * (w_max - w[0]_old) -
                   delta[0] * (w[0]_old - w[1]_old)
        hurdle[1] = hurdle[1] * learn   // switch off potentiation if learn == 0
        for each w[i], 1 < i < 4, in weight_vector do
          w[i]_new = w[i]_old + hurdle[i].value * alpha[i] * (w[i-1]_old - w[i]_old)
                     - delta[i] * (w[i]_old - w[i+1]_old)
                     // where w[i+1]_old = w_min, a constant, if i == 3

        // determine if the value of w_max should be raised (for associative adaptrodes
        // only.  if w3 has exceeded a fixed threshold value then marginally raise the
        // value of w_max (see above computation of w0).
        if w[3]_new > NONLINEAR_THRESHOLD then // compute new w_max value
          w_max_new = w_max_old + (1.0 - w_max_old) * w[3]_new -
                      NONLINEAR_DECAY_RATE * (w_max_old - w_max_base // from atype)
          // w_max will range between w_max_base and 1.0

      test for reset of learn switch; if input has fallen below MINSIGNAL (quiescent)
        and learn had been set to 1, then learn = 0

      // compute integration of this adaptrode's response with the rest of the adaptrodes
      if the adaptrode type is INHIBIT then
        neuron.sum = max(neuron.sum - response, 0)
      else neuron.sum = neuron.sum + (1.0 - neuron.sum) * response
      // note that this algorithm shunts the effects of adaptrodes as the value of sum
      // approaches 1.0, its maximum value
    // end each adaptrode
    if sum > threshold then output_new = sum
    else output_new = output_old - OUTPUT_DECAY * output_old  // exponential decay
      // where 0 < OUTPUT_DECAY < 1

    // compute threshold value (for dynamic thresholds)
    if threshold is to be modulated upward (rising) then
      threshold_new = threshold_old + threshold_alpha * (1.0 - threshold) *
         threshold_modulator_source.value -
         threshold_delta * (threshold - threshold_base)
    else if threshold is to be modulated downward (decreasing) then
      threshold_new = threshold_old - threshold_alpha * threshold *
         threshold_modulator_source.value +
         threshold_delta * (threshold_base - threshold)
    // threshold will range between 1 and threshold_base (up) or threshold_base and 0
    // (down)
  // end each neuron

  for each outslot[i] in outslot do
    get outslot[i].value from source neuron.output_old
    compute integer greyscale value as int(round(SIGNAL_MAX * output[i].value,0))
// end task

See Code (below) for details and supporting functions.

Atypes

Adaptrodes vary widely by types with regard to learning dynamics.  The atype structure is used to hold rate constants particular to a given adaptrode type.  An array of atypes is then used to compactly store the type information and is used by reference in the computation of each adaptrode (as above).  The current data stored in an atype structure is:

 int     id;          /* identification = array index */
 double  decay,       /* decay constant for adaptrode response */
         extinction,  /* decay rate for extinction */
         wt_max,      /* baseline or initial w_max */
         wt_min,      /* constant lower bound on w[3] */
         alpha[4],    /* increase rate constants */
         delta[4];    /* decay rate constants */
 

Ntypes

In a typical neural network there may be many different types of neurons.  Types are determined according to the nature and behavior of the threshold dynamics.  Threshold values can range between 0 and 1.  Three basic kinds of thresholds are supported in this version. In the first case the threshold remains fixed.  A threshold that increases with neuron output tends to damp the output with constant excitation.  Such a neuron requires increasing stimulation in order to keep firing.  The third type of threshold will cause a neuron to burst or fire more easily with decreasing stimulation.

The ntype object contains a set of rate constants which control the threshold behavior.  The current version contains the following variables:

 int      id,       /* identification = array index */
          US_src;   /* NEURON = n->out0, ADAPTRODE = a->response (usually a[0]) */
 double   t_decay;  /* threshold decay rate */
 double   t_alpha;  /* threshold increase rate */
 

Adaptrodes

The workhorse processing unit of this neural network, and the basis for all learning phenomena, is the adaptrode structure. In this version adaptrodes are used primarily for synapse processing.  However, adaptrodes can be used to modulate threshold values in some kinds of neurons.

Each neuron contains an array (dynamic) of adaptrodes.  For associative neurons, ususally, the 0th adaptrode is used as the unconditionable stimulus (US) receiver and hence the hurdle source for gating potentiation in all learning adaptrodes in the array.

Current structure of adaptrode:

 int     id,          /* identification = array index */
         atype_id,    /* index number of the atype for this */
         type,        /* 0 = fixed, 1 = excite, 2 = inhibit */
         learn,       /* state switch which allows w[1] gating */
         extinguish,  /* state counter to time missed expectations */
         src_type;    /* NEURON or SLOT (used in linking) */
 int     src_id;      /* index of relevant source type */
 double  *src,        /* pointer to source double value, e.g.,
                         NEURON -> neurons[src_id].out0
                         SLOT   -> inslots[src_id].value */
         response,    /* output response of this */
         w_max,       /* weight max variable for w[0] pull up
                         w[0] = w[0] + alpha[0]* *src->out0 *
                                (W_MAX - w[0]) - delta[0] * ... */
         w[4];        /* weight vector */
 Atype   *atype;      /* pointer to the atype record for this */
 long    age;         /* incremented each processing cycle
                         to be used in vertebrate brains */
 byte    record;      /* selection for recording */

This adaptrode computes a weight vector of up to four memory trace weight values.  These are immediate, short- (millisecond time constants), intermediate- (minute time constants) and long-term (hour time constants) memory respectively.  In addition, the adaptrode implements several important features to causal correlation learning.  The first is a strict requirement for temporal order between the arrival of the CS (learnable) signal and the US (unconditionable) signal.  The former must arrive and have achieved a minimum level of temporal integration prior to the arrival of the latter in order to permit the hurdling of the level 1 gate (see algorithm above).

The second feature is the implementation of extinction.  This is the higher rate of decay applied to the w[0] weight value in the case when a CS signal has been present for some amount of time (more than 1/2 second) and has not been followed by a US signal.  The extinction rate of decay is greater than normal decay on the weight.  This feature causes a learning adaptrode to have a diminished encoding of an expectation that the purported CS is a predictor of the US.

The third feature is the implementation of nonlinear learning, emulating the long-term increase in ion channel concentration in post-synaptic membrane when a synapse has been potentiated on a long-term basis.  This is accomplished by setting the w_max (pullup) variable to something less than one (maximum trace value).  This creates a weakened increase rate for potentiation but does not prevent potentiation to the w[3] level.  When the latter exceeds some preset threshold value (not to be confused with the neuron's firing threshold) w_max is, itself, potentiated, that is raised differentially.  Thus in future periods of input to the adaptrode, the pullup effect on w[0] is enhanced leading to stronger responses.  This effect represents long-term (permanent) memory trace.

All of these features as well as the number of active levels in a given adaptrode are controlled by state variables either in the atype object or within the adaptrode structure itself.

Neurons

Neurons are the main convergence processors for multiple CS/US signals. The basic function of a neuron is to perform a spatial integration of multiple input signals.  These may or may not encode causal correlations (learning).  In MAVRIC the majority of neurons do not learn or adapt to changes in convergences of signals.  In fact, only two neurons provide this function currently(see Associative layer in MAVRIC Brain Architecture).

The current contents of the Neuron structure:

 int       id,            /* identification = array index */
           ntype_id;      /* index of ntype */
 Ntype     *ntype;        /* pointer to ntype record */
 double    out0,          /* old out */
           out1,          /* new out */
           thresh,        /* axonal hillock threshold variable.
                             may be dynamic threshold. */
           t_base,        /* threshold base value used for dynamic
                             thresholds  */
           *t_up, *t_dwn, /* pointers to up/dwn modulator nodes */
           sum,           /* integration variable for result of
                             synaptic inputs */
           *reward,
           *punish,
           *confirm;      /* pointers to memory trace modulators */
 Adaptrode *synapses;     /* adaptrode array */
 int       phase;         /* life phase; 0=developmental */
 long      age;           /* incremented each processing cycle
                             to be used in vert. brain */

 int       adapt_cnt,     /* number of adaptrodes in the array */

           reward_src,    /* id of reward source node */
           reward_src_type,/* NEURON or SLOT */
           punish_src,    /* id of punish source for avoidance */
           punish_src_type,/* NEURON or SLOT */
           confirm_src,   /* id of confirmation (long-term reward) */
           confirm_src_type,/* NEURON or SLOT */
           t_up_src,      /* id of threshold up modulator node */
           t_up_src_type, /* NEURON or SLOT */
           t_dwn_src,     /* id of threshold down modulator node */
           t_dwn_src_type; /* NEURON or SLOT */
 byte      record;        /* selection for recording */
 

Inslots

The greyscale (0-255) value of inslots are set by external (body function) tasks, such as sensor transduction.  These tasks include sensing energy levels, food in the stomach, pain and damage and, potentially, other body state variables.

The current inslot structure:

 int        id;            /* identification = array index */
 int        greyscale;     /* sensor input 0 - MAXGREYSCALE */
 double     value;         /* greyscale / MAXGREYSCALE */
 byte       record;        /* selection for recording */

Outslots

Outslots get real valued output from target neurons (output neurons), typically motor or endocrine.  The slot converts the real value to an integer greyscale for use by external (body function) tasks such as setting motor speeds.

The current outslot structure:

 int        id;           /* identification = array index */
 int        greyscale;    /* (int) (value * MAXGREYSCALE) */
 double     value;        /* output from a neuron out0 */
 int        neuron_id;    /* index of source neuron */
 double     *src;         /* pointer to neuron out0 */
 byte       record;       /* selection for recording */

Code

The C source code for the brain program is available here.

This material is based upon work supported by the National Science Foundation under Grant No. IIS-9907102.

Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author and do not necessarily reflect the views of the National Science Foundation.