2. Heat Capacity
3. Thermal Conductivity
4. Viscosity
5. Vortex / Rotational Viscosity
6. Thermal Expansion Coefficient
7. Pyromagnetic Coefficient
8. Time Constant
9. Magnetic Susceptibility

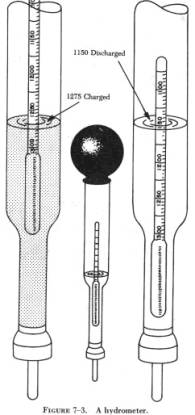
Most hydrometers are calibrated at 60°F and sample temperatures
deviating from this need correction.The chart below contains the correction
factors to add to the specific gravity reading.
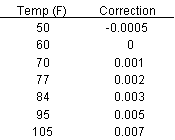
The density can also be simply measured using a volumetric flask and mass balance.
DENSITY OF MAGNETIC FLUIDS
Experimental results, like those in the comparison table, show that the ferrofluid has a higher density than its carrier fluid.Density increases as the volume fraction of solid particles increases in the colloidal mixture.If the volume of the colloidal mixture is assumed to be the same as the sum of all the volumes of the components, the density is represented as

If we further assume that the density of the surfactant and carrier fluid are approximately the same the previous equation reduces to
A common way to find the volume fraction of the solid phase is using this equation.
|
|
|
|
|
|
| Greek
Letters
r=density f=volume fraction fn=hydrodynamic volume concentration |
Subscripts
s=solid (magnetic) phase a=surfactant f=carrier liquid |
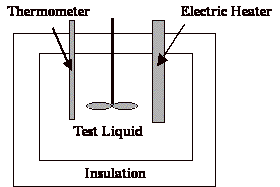
Heat capacity is determined by a calorimeter.It can be deduced from the equation E=mCpDT.E is the energy put into the calorimeter, m is the mass of sample in the calorimeter, Cp is the heat capacity, and DT is the change in temperature.Data is obtained such that Cp is the only unknown in this equation.
The mass (m) of the test liquid put into the calorimeter is known.The energy (E) is determined by multiplying the potential by current over the time it runs (E=V*I*t).Temperature rise (DT) is recorded via the thermometer.
HEAT CAPACITY OF FERROFLUIDS
Assuming the molecular
interactions greatly exceed those of particle-particle the heat capacity
can be represented using the mixing rule.
In our case the heat capacity of the magnetic solid is much less than that of the fluid or surfactant.Thus, an increase in mass concentration of the solid particles will cause the overall heat capacity of the ferrofluid to decline.
Berkovsky mentions that
the validity of this expression is backed by experimental data.
|
|
|
|
|
|
| C=heat
capacity (specific heat)
Y=mass concentration |
Subscripts
m=magnetite a=stabilizer f=liquid base |
Hot wire technique uses two wires to measure the conductivity.One generates thermal energy and the other is used as a thermocouple.They are placed a known distance apart in a sample and are not moved.Once the system is started the temperature is recorded vs time at a constant q output from the heater.The conductivity is determined from the plot DT vs. t.
THERMAL CONDUCTIVITY OF FERROFLUIDS
When we add magnetic particles to a carrier fluid the conductivity of the mixture increases.This is expected because the thermal conductivity of the magnetic particles being added can have 10-100 times higher conductivities than the carrier fluid.Obviously, since the conductivity of the magnetite is so high compared to that of the carrier liquid, increases in its volume fraction are bound to have a dramatic effect.
Experimental data of conductivity
vs. volume fraction of the solid phase yields a straight line.(See Berkovsky
(1993) pg. 49.)This line, empirically fit to the data, yields a maximum
error of 5%.
![]()
Berkovsky suggests that
when lf<<lm
and fs<<1 ![]() be used.No information was found regarding how smallfs
or lf compared
to lm should be.
be used.No information was found regarding how smallfs
or lf compared
to lm should be.
|
|
|
|
|
|
| l=thermal conductivity | Subscripts
s=solid (magnetic) phase a=surfactant f=carrier liquid |
The viscosity of a magnetic fluid depends on the solid fraction f, the viscosity of the carrier fluid h0 and the applied magnetic field (orientation as well as force).
For the determination without an applied magnetic field every standard viscometer can be used. In addition the viscosity can be estimated using one of the following formulas (from Rosensweig, ãFerrohydrodynamicsä):
small particle concentration
![]()
higher particle concentration:

fc = 0.74 (closed package)
Experiments to determine the viscosity with an applied magnetic field where conducted by McTague (1969) with a capillary tube viscometer. The result of this experiments is shown in the figure below and can be expressed with the following formulas:
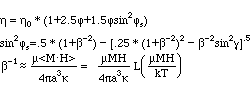
L: Langevin function
g : angle between axis of rotation of the fluid and H
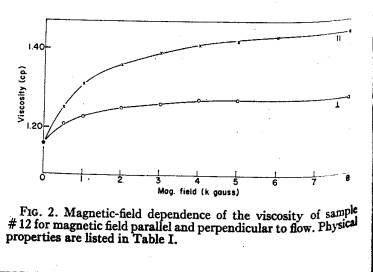
McTague, J. Chem. Phys., vol. 51, no. 1, 1969, p. 133-6
The rotational or spin viscosity of a ferrofluid describes the dampening
through internal rotational friction. It can be measured using a torsional
pendulum by determination of the
resulting deflection amplitude for different frequencies.
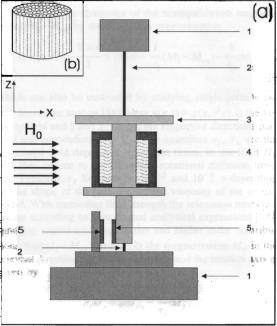

Furthermore it can be estimated using the following equation
or be estimated with the following equation derived by Shliomis (1972):
Definition:
![]()
Typical value
Shell oil7.17 ´10-4
Ferrofluid7.17´10-4
Measurement method
Use the instruments such as following to measure it
directly.


Linear Thermal Expansion measurements from -80°C
to +1600°C in air, argon, nitrogen or vacuum.
http://www.theta-us.com/about.html
Calculation from the properties of its components:
![]()
where bs, ba, bf
are the thermal expansion coefficients of particles, a stabilizer and a
carrier-liquid.jis
volume fraction.
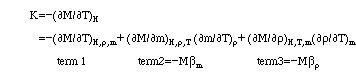
WhereMmagnetization of magnetic fluids;
Hmagnetic strength;
Tabsolute temperature;
mmagnetic moment of a particle;
Typical
value
In the case of strong fields(![]() >>1),
the fluid is in a state of magnetic saturation and despite the Brownian
movement all the magnetic moments of particles are aligned along a magnetic
field. Therefore, the Brownian movement doesnât not contribute to
the temperature dependence of magnetization and the first term in above
equation is equal to zero. Then, for a pyromagnetic coefficient:
>>1),
the fluid is in a state of magnetic saturation and despite the Brownian
movement all the magnetic moments of particles are aligned along a magnetic
field. Therefore, the Brownian movement doesnât not contribute to
the temperature dependence of magnetization and the first term in above
equation is equal to zero. Then, for a pyromagnetic coefficient:
![]()
Far
from the Curie temperature the quantity bm
is very small and for magnetic fluids it may be neglected. This implies
the pyromagnetic coefficient of the magnetic fluid, being in the saturation
state, is determined only by ![]() . For
most situations,
. For
most situations,
In the case (![]() <<1),
<<1),
![]()
At the room temperature, it
has the order of 3´10-3K-1
FerrofluidK=12;
Measurement
method
Definition
The time of onset of equilibrium concentration is
determined by the characteristic time of diffusion ![]()
Magnetic susceptibility is a quantitative
measure of the extent to which a material may be magnetized in relation
to a given applied magnetic field. The magnetic susceptibility of a material,
commonly symbolized by c,
is equal to the ratio of themagnetization M within the material to the
applied magnetic field strength H, or c
= M/H. This ratio, strictly speaking, is the volume susceptibility, because
magnetization essentially involves a certain measure of magnetism (dipole
moment) per unit volume.
Magnetic materials may be classified
as diamagnetic, paramagnetic, or ferromagnetic on the basis of their susceptibilities.
Ferromagnetic materials, such as iron
and cobalt, do not have constant susceptibilities; the magnetization is
not usually proportional to the applied field strength. Measured ferromagnetic
susceptibilities have relatively large positive values, sometimes in excess
of 1,000. Thus, within ferromagnetic materials, the magnetization may be
more than 1,000 times larger than the external magnetizing field, because
such materials are composed of highly magnetized clusters of atomic magnets
(ferromagnetic domains) that are more easily lined up by the external field.