Thermal Conductivity

 

Of Ferrofluids

 

 

 

Matthew Bernards

Chem E 499

6/7/01

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Table of Contents                                                                                                     Page

 

1.     Introduction                                                                                                             2

2.     Experimental Design                                                                                                2

3.     Materials                                                                                                                  6

4.     Procedures                                                                                                               7

5.     Early Troubles                                                                                                         8

6.     Determination of Steady State Time                                                                       9

7.     Results                                                                                                                     10

8.     Discussion                                                                                                               11

9.     Recommendations                                                                                                    13

10.  Conclusions                                                                                                             14

11.  Nomenclature                                                                                                           14

12.  Literature Cited                                                                                                        15

13.  Appendices                                                                                                             

            A.  Apparatus                                                                                                    16

            B.  FIDAP Results                                                                                            18

            C.  MATLAB Code – Steady State Approximations                                       20

D.   Time to Steady State Data                                                                           21

E.    Experimental Data and Results                                                                    24

F.    Data from Trouble Shooting Period                                                             27

Introduction

            The uses of ferrofluids have become quite diversified in the recent years.  One use for these fluids is heat removal in transformers.  The fluids fill the internal compartments of the transformers near the coils and help remove the heat with both conduction and convection.  The purpose of this study was to determine the thermal conductivity of pure and diluted ferrofluids, to further understand their heat removal properties in transformers.  The ferrofluid that was tested is a 45 gauss oil based fluid.

 

Experimental Design

            Before thermal conductivity testing could begin, an apparatus for measuring the thermal conductivity needed to be designed.  The basis for this design was taken from Smith [1] and his groundbreaking research measuring the thermal conductivities of several liquids in the 1930s.  The original apparatus used by Smith consisted of two concentric copper cylinders with a gap of 1/64 of an inch between.  The fluid of interest was placed in this gap and the entire apparatus was heated from the center copper cylinder with a high resistance wire, located in the center of this cylinder.  The heat removal was accomplished by placing the entire set-up into a constant temperature oil bath.  For further details on this work please refer to Reference 1, at the end of this paper.

            A new apparatus was designed for this testing, patterned after Smith’s experimental set-up.  The main differences consisted of upgrades in the electronics and theoretical calculations of the dimension and components.  The first of these theoretical calculations was a simulation of the temperature distribution for one quarter of this apparatus.  This simulation was completed with the PDE toolbox on MATLAB.  This simulation represented one corner of the apparatus and it is identical for all four corners.  Because it is the same for all four corners the simulation could be run for only one corner making the simulation easier to run and interpret.

            In this simulation it can be seen that there are four blocks.  The top three represent the inner copper cylinder, the fluid gap, and the outer copper cylinder from left to right. The large lower block represents the plexiglass cover and it was given a thermal conductivity of 0.2 W/m K.  The copper blocks and fluid were assigned thermal conductivities of 400 W/m K and 0.2 W/m K respectively.  The boundary conditions that were assigned to these blocks were simple approximations, to determine what the general temperature distribution trends would be.  The plexiglass block was assigned adiabatic surfaces on the bottom, top, and left.  The entire right hand side of the diagram was assigned a temperature equal to 0.  This temperature value was also used for the top of the outer copper block.  The fluid gap block was given a linear temperature distribution across it, and the other copper block was assigned a temperature equal to 1.  These boundary conditions are summarized below, in Figure 1.

 

 

 

 

 

 

 

 


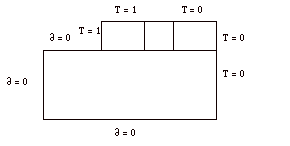
Figure 1: Boundary Conditions for Simulation

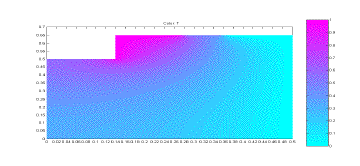
            The simulation was run under these conditions to see the overall heat distribution trends.  The purpose of this simulation was to see if plexiglass would be an effective way to prevent the loss of heat from the top and bottom of the apparatus.  The planned calculation method included the assumption that there was no heat loss from the top and bottom of the apparatus, and this simulation would test that assumption.  The simulation results can be seen below, in Figure 2.

 

 

 

 

 

 

 

 

Figure 2: Simulation of Apparatus Temperatures

            From the simulation results it can be seen that there is basically no temperature change on the lower and outer surface of the plexiglass cover.  There is some temperature change on the left side of the plexiglass, but this is only the midpoint of the apparatus and the simulation results for the other half would be a mirror image of this.  Based on this simulation, it can be seen that the assumption of no heat loss from the plexiglass is a justifiable one.

            The next simulation study that was completed was done to determine the dimensions of the apparatus.  This simulation was completed with FIDAP code written by Professor Finlayson.  This code simulated a two dimensional fluid gap, modeled as a plane.  The purpose of this simulation was to determine at what point convection effects came into play in this heat transfer process for an apparatus with a height value of 1 and a width value of 1/64, which represented the dimensions of the apparatus found in Smith’s work [1].  The Nusselt number was calculated by this program, for varying Prandtl and Rayleigh numbers.  The Nusselt number is a measure of the convective heat transfer occurring at a surface and when it is less than or equal to one, it means that there is negligible convective heat transfer taking place within the substance [2].  This simulation was run for Rayleigh numbers ranging from 10-3 to 105 and Prandtl numbers equal to 0.71, 1, 10, and 100.  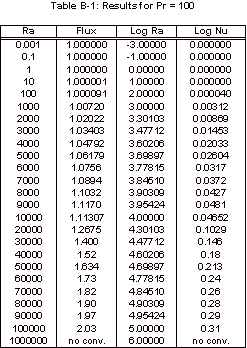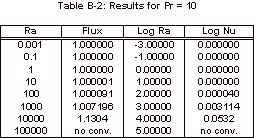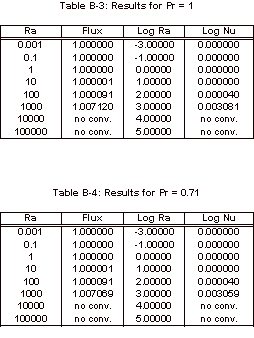The results obtained with this simulation can be found in Appendix B and the corresponding graph of these simulation results can be seen below, in Figure 3.

 

 

 

 

 

 

 

 

 

 

 


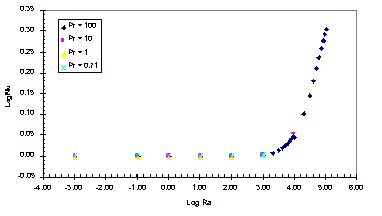
Figure 3: Nusselt Number Relationships

 

            As can be seen in Figure 3, the Nusselt number does not vary from one until the Rayleigh number increases past 1,000.  It can also be noted that the Nusselt number shows no variation over the four Prandtl numbers that were tested.  The magnitude of the Rayleigh number that is expected for our experiment is on the order of 1, so based on this simulation it is known that there will be relatively no convective heat transfer within our fluid sample for the length to width ratio of 1:1/64.

            The last computer simulation that was completed was another MATLAB simulation.  This theoretical calculation was completed to estimate the steady state time it would take to achieve a certain temperature change across the fluid.  This simulation, written by Professor Finlayson, was used to simulate a heat flux of 1.5 W.  This value and all of the others used in the code were all approximations of the actual experimental parameters, including an estimated thermal conductivity for the oil.  These values were used in order to tie this simulation to our experimental work as closely as possible.  The final simulation results can be seen below, in Figure 4 (This is revised from the original).

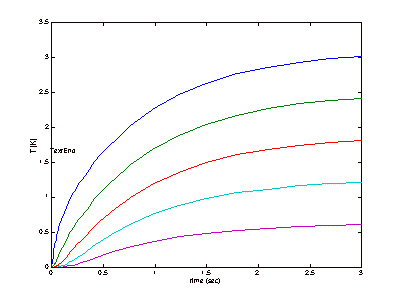
Figure 4: Steady-State Approximations

 

            It can be seen in Figure 4 that the apparatus will be expected to reach steady state very quickly.  It is likely, however, that this simulation did not completely account for all of the variables that could affect each trial run, so the time to steady state was also tested experimentally and this will be discussed later.

            The design simulations were completed with conclusion of this final test.  The apparatus was designed so that there would be no convection effects in the fluid sample, based on the FIDAP simulation and it was designed to have no heat losses out of the ends, based on the results of the first MATLAB simulation.  The final simulation showed that the apparatus would reach steady state in a relatively quick manner, as seen by the extremely small steady-state times, but this was verified experimentally as well.

 

Materials

The final design consisted of two concentric copper cylinders capped on the top and bottom with plexiglass.  A schematic of this apparatus can be seen in Appendix A.   Although not seen in the apparatus schematic, a 1/8 inch copper pipe was wrapped around the outer copper cylinder.  Water was run through this pipe when operating the apparatus, in order to remove the heat being produced by the heater.  Leakage from the fluid gap was prevented by placing two gaskets on each cap, around the portion of the cap that protrudes into the fluid gap.  These caps were held into place with plastic screws, allowing the lids to be held on tightly, while allowing for easy removal to clean and fill the fluid gap. 

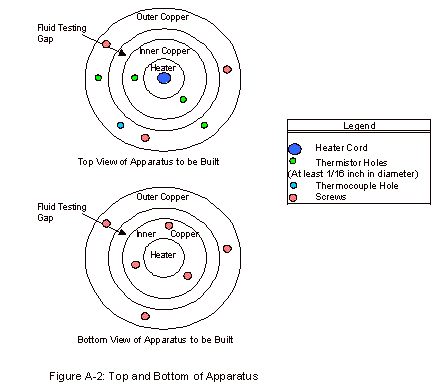
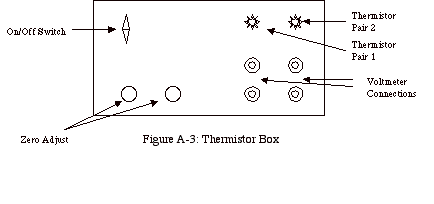
As can be seen in Figure A-2, in the Appendix, there are four holes present in the top for thermistors.  These thermistors are paired and allow for fairly accurate measurements of the temperature difference across the fluid gap.  This measurement is repeated, as it is one of two key experimental values, presenting a way to determine the accuracy of this measured temperature difference.  If the values for the two are largely different, something is not working correctly in the apparatus and the trial results are not accurate.  These thermistor measurements are output as electronic signals, which are monitored by a voltmeter.  The conversion of this voltage to a temperature is as follows:

DT = V / 8.6 mV/oC                            (1)

In Equation 1, T is the temperature in Celsius and V is the voltage measured in mV.  This equation is derived based on the thermistor’s power source and the resistance network between pairs of thermistors.

 The other key experimental measurement is the voltage being input into the heater.  With this value the heat flux can be calculated as follows:

q = V2/R                                              (2)

In Equation 2, q is the heating rate in watts, V is the AC voltage input to the heater, and R is the resistance of the heater in ohms.  With the current set-up, a current of about 45 volts is being used, through a heater with a resistance of 1413 ohms.  This gives us a heating rate of about 1.4 watts, as calculated with Equation 2.

            With values for both the temperature difference and the heat flux, one can easily calculate the thermal conductivity.  The equation for this is [2]:

k = q ln(r2/r1) / 2pLDT                        (3)

In Equation 3, k is the thermal conductivity in W/m K, q is the heating rate in watts, r1 and r2 are the inner and outer radii respectively, L is the height of the apparatus in meters, and DT is the temperature difference across the gap in Kelvin.

The thermocouple hole, which can be seen in Figure A-2, was present in order to determine the temperature of the outer copper block.  With this temperature and the temperature difference, the inner copper cylinder temperature could also be calculated.  This value was taken for record purposes, as thermal conductivities vary sometimes with temperature

 

Procedure

            The procedure for this experiment is not overly complicated.  First, the lower part of the apparatus is assembled.  This includes placing the gaskets onto the bottom plexiglass and screwing this piece into place.  Once this has been completed, the fluid is loaded next.  This is done using a syringe.  The fluid should be loaded slowly, around the entire gap until it begins to come out of the top.  The fluid coming out of the top indicates that the fluid gap is completely filled.  At this point the heater is inserted, the top gaskets are put into place, and the top cap is screwed on.  Next, both thermistor pairs are zeroed using an Icell constant temperature cell.  After zeroing them, the thermistors are coated in Thermalcote and put into place.  Thermalcote is a high thermal conductivity paste, which allows for good contact between the thermistors and the copper.  The thermocouple is also put into place at this time.  The cooling water flow is begun next, upon completion of the assembly.  Once this flow is begun, the heater is turned on and the apparatus is allowed to heat to steady state.  Steady state is achieved when the thermistor measurements have stabilized.  Once this has occurred, the steady state temperatures and heater voltage are recorded, completing the experimental data collection for the calculation of that fluid’s thermal conductivity.

            Clean up for this apparatus is very similar to the setup.  The thermistors and thermocouple are first removed and wiped off.  Next the top and the heater are removed.  The fluid is drained and collected by removing the outer three screws from the bottom and pulling the inner copper cylinder out.  Once the fluid is removed, the entire apparatus is wiped down and cleaned, to remove any residue from the fluid that was just tested.

 

Early Troubles

            The first stage of the experimental testing was a verification of the accuracy of the results that could be obtained with the apparatus.  In order to do this, water was tested a number of times.  The initial results with the water were very inconsistent and inaccurate and as a result modifications were made in both the procedure and some of the electronics.  Different procedures that were tried included varying the length of trial runs, varying the cooling water flow rate, and trying a constant temperature water bath as the cooling method.  Over the course of these trials it was determined that the length of trial runs seemed to be an important variable, but the cooling water flow rate did not.  It was also determined that a constant temperature water bath did not yield results that were any more accurate than those obtained with the cooling water flow.

            Over the course of these initial trials, many of the apparatus’ bugs were determined and removed as well.  One of the first improvements was the use of Thermalcote for the thermistors.  This substance eliminated air convection in the thermistor hole, which was causing the temperature reading to fluctuate substantially.  Another improvement that was made to help eliminate drift in the thermistors was a redesign and upgrade of their resistor system.  Finally, there were a number of improvements in the equipment itself.  One pair of thermistors continually gave extreme results and that pair was eventually replaced.  After a time, the heater burnt out and needed to be replaced as well.  The data and resulting thermal conductivities corresponding to all of this initial work can be found in Appendix F.

 

Determination of Steady State Time

            One of the simulations that was run during the design phase of the research was a MATLAB simulation to determine the steady state time.  This simulation yielded a steady state time of 1x10-5 seconds.  This was seemingly extreme, as steady state did not appear to be occurring in any of the experimental trials for at least forty-five minutes.  As a result of these contradicting results, it was determined that the steady state behavior needed to be studied more closely.  This study was conducted after the heater had been replaced in the trouble shooting portion of the data collection.

            The procedure for determining the steady state time was very basic.  Temperature measurements were taken with the thermocouple and both thermistor pairs every minute for the first five minutes and then every two or three minutes for approximately thirty minutes total.  These measurements were taken for one trial with water and two with octane and the results for one of the octane trials can be seen below, in Figure 5.

 

 

 

 

 

 

 

 

 

 

 


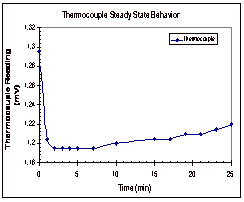
Figure 5: Steady State Trends for Octane

 

 

            In Figure 5, it can be seen that the thermistors appear to reach their steady state values within five minutes of the start time.  The thermocouple, on the other hand, shows a continual increase in temperature over time.  These trends were seen in the other two trials as well and the results from these two trials can be found in Appendix D, along with the data that was collected experimentally.

            Based on the results of these experimental runs, it was determined that the thermocouple was not a good way to determine if the temperature had reached steady state across the fluid gap.  It was seen in all three trials that the temperature difference between the two copper cylinders reached its steady state value long before the thermocouple even neared its steady state value.  Based on this, it was decided that trials would be run for ten to fifteen minutes, until the thermistor readings reached their steady state range.

 

Results

            The ultimate goal of this research was the determination of the thermal conductivity of a 45 gauss ferrofluid.  The apparatus’ accuracy was tested prior to testing the ferrofluid itself, by running experiments with octane and water.  The thermal conductivity of the ferrofluid over a range of concentrations was measured as well.  All of the average thermal conductivities can be found summarized in Table 1, below and the corresponding data along with each individual trial’s results can be found in Appendix E.

Table 1: Summary of Calculated Thermal Conductivities

Fluid*

Number of Trials

Thermal Conductivity (W/mK)

Standard Deviation (W/mK)

Water

3

0.442

0.109

Octane

6

0.117

0.005

Base Oil

3

0.106

0.001

80/20 Mix

3

0.109

0.001

60/40 Mix

3

0.114

0.002

40/60 Mix

3

0.111

0.004

20/80 Mix

3

0.112

0.003

45 G Ferrofluid

3

0.113

0.001

*Mixtures represent Base Oil/45G mixtures.

The results obtained by varying the concentration of the mixture were also plotted to show the relationship between concentration and thermal conductivity.  This plot can be seen in Figure 6, below.

 

 

 

 

 

 

 

 

 

 

 


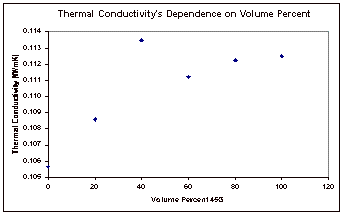
Figure 6: Concentration Dependence of Thermal Conductivity

 

Discussion

            In order to determine the accuracy of the newly designed apparatus two fluids were tested to see how their calculated thermal conductivities compared to their literature values.  The literature value for the thermal conductivity of octane is 0.128 W/mK and for water it is 0.598 W/mK, both taken at 20° C [3,4].  Comparing these values to those obtained experimentally, it can be seen that the apparatus is yielding results that are slightly lower than the literature values. 

            In looking at the calculated value for the thermal conductivity of water, it can be seen that the results are neither accurate nor precise.  There was a lot of variation in the results obtained with the different trials, which let to an extremely large standard deviation, 0.1 W/mK.  The inability to obtain consistent results with the water can likely be attributed to a few things.  One factor to consider is the surface tension of the water.  The fluid gap was fairly small, and it is possible that the water did not completely fill the gap.  It is also possible that the water could have filled portions of the gap unevenly, further affecting the results.  Another possible error associated with the water could be its source.  Tap water was used for all of the trials and it is very possible that the water could have had any number of contaminants in it.  These could have varied from day to day as well, resulting in further inconsistencies in the measured thermal conductivity.

            The octane results were much more accurate than those obtained with the water.  If should be pointed out that there was one outlying trial out of the six that were run and if that trial is removed from the average thermal conductivity calculation, the value rises to 0.119 ± 0.001 W/mK.    This new average value is even closer to the literature value and it also has a smaller standard deviation, attesting to the consistency of the trials with the exception of the one outlying trial.  These trials were also carried out over a variety of voltages, proving that the results obtained with this apparatus were repeatable even while varying the experimental parameters.  Based on the results obtained for octane, it was decided that the apparatus would be an acceptable method for testing the thermal conductivity of the ferrofluid.

            The ferrofluid itself was then tested, to determine its thermal conductivity.  As can be seen in Table 1, the thermal conductivity of the 45G ferrofluid is 0.113 ± 0.001 W/mK.  This average is based on the results of three independent trials, and based on the octane results it should be within 0.01 W/mK of the actual value.

            The final results that were obtained were the thermal conductivity’s dependence on concentration.  It was expected that this relationship would be linear, but this does not appear to be the case with the results from this experiment, as seen in Figure 6.  With the exception of one outlying point, it appears that this dependence is actually a second order relationship.  Excel was used to fit best fit lines and second order curves to both the original data and the data with the outlying point removed, and the equations for these fits and the correlation coefficients (R2) can be found on the next page, in Table 2.  The trendlines themselves can be seen with the corresponding data points in Appendix E also.

            Based on the correlation coefficients, it can clearly be seen that a second order equation fits the results much better than the linear fit.  This can be seen in the results for both data sets.  Of course the data with the outlying point removed yield much a substantially better fit as compared to the results that were obtained with that point included.

 

Table 2: Trendline Equations

Graph Fit

Equation

Correlation Coefficient
All Data, Linear

6´10-5 X + 0.1076

0.6031

All Data, Second Order

-1´10-6 X2 + 0.0002 X + 0.1058

0.8313

Point Removed, Linear

7´10-5 X + 0.1065

0.9299

Point Removed, Second Order

-7´10-7 X2 + 0.0001 X + 0.1058

0.9944

 

            The source of error that created the outlying point is uncertain.  It is possible that there was an error in making up the solution, but this is not very likely.  This is due to the fact that the calculated thermal conductivity is larger than that for the pure ferrofluid, which is has the highest possible thermal conductivity for any combination of it with the base oil.  Another possible source of error could have been some impurity that got into this solution before or after it was made up.  This impurity could have caused the thermal conductivity value to be much higher than the mixture’s actual thermal conductivity.  This error source is supported by the fact that the different trials were fairly precise, pointing to some form of error in the mixture itself.

 

Recommendations

            The results that were obtained with this apparatus appear to be fairly precise and accurate.  The standard deviations that were obtained for all of the ferrofluid trials were smaller than the expected accuracy of the apparatus that was determined from the octane results (0.01 W/mK).  For this reason there are very few upgrades that are recommended for the equipment.  The main upgrade that is recommended is a new method for feeding the cooling water.  Currently there is a small reservoir connected by tubing to the coil inlet.  The reservoir requires continual filling throughout the duration of the experiment and the procedure could be simplified if a pump system or larger reservoir were invested in.  The best possible alternative is a pumping system that could recycle the water continuously.  This would prevent constant refilling of the reservoir, aiding the operator immensely.  A larger reservoir is another alternative, but this could create problems, as it is possible that the flow rate would vary over time depending on the liquid level in the reservoir.

            Based on the results that were obtained, there are two fluids that require additional testing.  The first fluid that should be examined more closely is water.  Additional tests should be run with distilled water, in order to determine why consistent results were not obtained with water initially.  Distilled water would help determine if the tap water itself was the source of the inconsistencies or if it was some aspect of the apparatus or procedure.  The other fluid that needs to be retested is the 40 percent 45G, 60 percent base oil mixture.  This was the outlying point in the concentration graph.  Retesting this mixture would result in a more accurate data point on the concentration curve, further showing the relationship between thermal conductivity and concentration.

 

Conclusions

            Based on the results obtained experimentally, this apparatus is an effective way to test the thermal conductivity of a liquid.  The apparatus appears to be accurate to within 0.01 W/mK as seen with the octane trial results.  It can also be concluded that the thermal conductivity of the 45G ferrofluid is 0.113 ± 0.001 W/mK, based on the experimental results.  The final conclusion that can be made from the experimental results is that thermal conductivity has a second order dependence on concentration, as seen in the plot of these two.

 

Nomenclature

q = Heating Rate [=] W

V = Voltage [=] AC

R = Resistance [=] W

k = Thermal Conductivity [=] W/m K

r1, r2 = Radius [=] m

L = Height of Apparatus [=] m

T = Temperature [=] oC or K

 

 

Literature Cited

1.     Smith, J. F. Downie. “Thermal Conductivity of Liquids.”  Industrial and Engineering Chemistry.  Volume 22, No. 11.  1930.

2.     Incropera, Frank P. and DeWitt, David P.  Introduction to Heat Transfer.  John Wiley & Sons, New York, 1996.

3.     Green, Don W.  Perry’s Chemical Engineers’ Handbook.  McGraw-Hill, New York, 1997.

4.     Lide, David R.  CRC Handbook of Chemistry and Physics.  CRC Press, Boston, 1991.

 

Appendix A: Apparatus

 



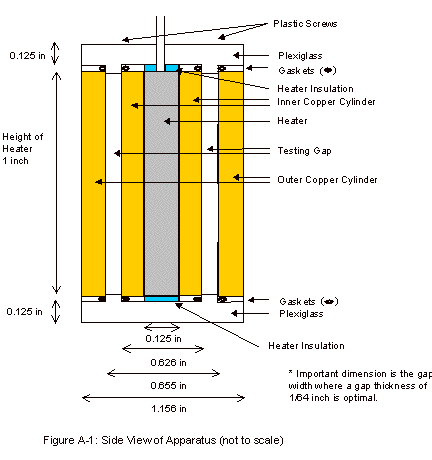
Appendix A: Apparatus


 

 




Appendix B: FIDAP Results


 

 

 

 

 


Appendix B: FIDAP Results

 


 

 

 

 

 

 

 

 

 

 

 

 



Appendix C: MATLAB Code – Steady State Approximations

 

% filename run3_ht.m

% run the transient heat transfer experiment

% alpha is thermal diffusivity, Qdot is the heating rate

% k is the thermal conductivity, t0 is the outer temperature

% r1 is the inner radius and r2 is the outer radius

 

global a1 a2 a3 a4 r1 t0 dr n

n = 15;

r1 = 0.0079502;

r2 = 0.0083185;

dr = (r2-r1)/n;

alpha = 0.03;

L = 1;

Qdot = 1.5;

k = 0.6;

t0 = 300.;

a1 = alpha/(dr*dr);

a2 = dr/2;

a3 = Qdot*alpha/(k*pi*r1*L*dr);

a4 = a3*dr/(2*r1);

 

y0 = t0*ones(1,n);

tspan = [ 0 0.00002];

[t,y] = ode23s('rhs3_ht',tspan,y0);

plot(t,y)

xlabel('Time (s)')

ylabel('T (K)')

title('Fluid Temperature Change (Q=1.5 W)')

 


% filename rhs3.m

 

function ydot=rhs2(t,y)

global a1 a2 a3 a4 r1 t0 dr n

 

row(1) = 2*a1*(y(2)-y(1)) + a3 - a4;

for i = 2:n

      if (i<n)

            yplus = y(i+1);

      else

            yplus = t0;

      end

      row(i) = a1*((yplus-2*y(i)+y(i-1)) + a2*(yplus-y(i-1))/(r1+i*dr));

end

ydot = row';