Last updated: January
4, 2000
Note: These notes are preliminary and incomplete
and they are not guaranteed to be free of errors. Please let me know if
you find typos or other errors.
- Nominal Variable
- A variable that is measured in current prices
- Example
- Nominal GDP in 1998 is measured in 1998 prices.
- Real Variable
- A variable that is "adjusted for inflation". More formally, a real variable is
measured in the prices of a chosen base year.
- Example
- The current base year for computing real GDP is 1992. Hence, real GDP in 1998 is
computed using the prices that prevailed in 1992.
- Variable Weight Price Index
- Value of current output at current prices divided by the value of current output at base
year prices.
- Example - GDP Deflator
- GDP Deflator = 100*(Nominal GDP)/(real GDP)
Nominal and real GDP |
| Year |
Nominal GDP
(billions of current $) |
GDP Deflator
(1992 = 100) |
Real GDP
(billions of 1992 $) |
| 1990 |
5,546.1 |
93.7 |
5,919.0 |
| 1991 |
5,724.8 |
97.3 |
5,883.7 |
| 1992 |
6,020.2 |
100.0 |
6,020.2 |
| 1993 |
6,343.3 |
102.2 |
6,206.8 |
| 1994 |
6,738.4 |
104.3 |
6,460.6 |
| Source: Survey of Current Business, July 1994 and
August 1995. |
- Fixed Weight Price Index
- Value of a fixed basket of goods at current prices divided by the value of the same
fixed basket of goods at base year prices.
- Example - Consumer Price Index (CPI)
-
Operationally, we compute real variables using the following formula
Real Variable = 100*(Nominal variable)/(Price
Index)
where the price index is defined to be equal to 100 in the chosen base year.
- Inflation
- Rate of growth of the genearl price level. Specifically, inflation over a time period is
calculated as the percentage change in a particular price index from one time period to
the next:
inflation = pt+1
= %DPt+1 = (Pt+1 - Pt)/ Pt.
Bond Prices and Interest Rates
Consider an investment in a one year T-Bill (default free pure
discount bond) that pays $10,000 = P1 one year from today. You buy the
bond today, at auction, for P0 = $9,708.74. The annual nominal interest rate on the
bond is defined to be the nominal rate of return on the investment:
i = (P1 - P0)/P0
= ($10,000 - $9708.74)/$9708.74 = 0.03
Thus the nominal interest rate on the T-bill is 3% per year.
Present value and future value
The rate of return equation can be rearranged to give the
following equations:
Future value: P1 = P0(1
+ i); e.g., $10,000 = $9708.74*(1.03)
Present value: P0 = P1/(1
+ i); e.g. $9708.74 = $10,000/1.03
The future value calculation says that today's value of $9708.74
grows to the future value of $10,000 when the interest rate is 3%. The present value
calculation says that $10,000 to be received one year from today is only worth $9708.74 in
today's dollars. The present value calculation clearly states that $1 today is worth more
than $1 to be received one year from today since the $1 today can be invested in a default
free bond paying 3% so that one receives $1.03 one year from today.
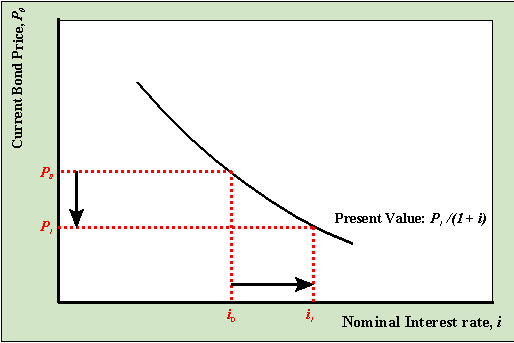
Inverse relationship between bond prices and
interest rates
The present value representation of the bond price shows that
there is an inverse relationship between bond prices and nominal interest rates: As i
increases, P0 decreases; as i decreases, P0
increases.
The Real Interest Rate
- Real interest rate
- The nominal interest rate adjusted for inflation.
Continuing with the example above, suppose that the annual inflation rate is 3%. The
investment in the bond returns 3% but overall prices have increased by 3% as well. Hence,
the investment in the bond has not increased the purchasing power of my money at all. I
have 3% more dollars but everything is 3% more expensive on average.
Calculating the real interest rate
Method 1 (Brute Force)
- Convert all nominal variables to real variables
- Compute rate of return on investment using real variables
For example, suppose the CPI today is 1 (this year is the base year) and next year it
turns out to be 1.03. Then the inflation rate over the year is 3%. The real rate of
return, r, on the bond using real variables is computed as
r = ($10,000/1.03 - $9708.74/1)/($9708.74/1) = 0.00
Thus the real rate of return is 0%.
Method 2 (Fisher Equation)
(annual) real interest rate = (annual) nominal interest rate - (annual)
inflation rate
r = i - p
In the above example, i = 3% and p = 3%
so that r = 3% - 3% = 0.
Expected Real Interest Rate
When individuals or firms make investment decisions, the true rate of inflation over
the future investment horizon is not known with certainty and so the true real rate of
return is not known with certainty. However, agents in the economy form expectations of
the future rate of inflation and so they have expectations of the real rate of return on
an investment. Given expectations of future inflation, we can define the expected real interest rate as
expected real interest rate = nominal interest rate - expected inflation
rate
re = i - pe
The superscript "e" denotes that the variable is an expectation of a
future variable. Notice that r = re only if p = pe ; i.e.,
only if expectations turn out to be correct.

