Our work is on the nonlinear dynamics of neurons, neural networks, and neural populations. These dynamics are beautiful, and are richly varied from setting to setting – at times governed by mechanisms we can distill and explain and at times eluding our best analytical tools. Beyond explaining the emergent dynamics of neural circuits, we want to understand how they encode and make decisions about the sensory world. Making progress on these twin problems requires a range of perspectives and methods. We delight in collaboration with fellow theorists of many different backgrounds, and with cognitive neuroscientists, clinicians, and electrophysiologists. Our methods blend data analysis, dynamical systems, stochastic processes, and information theory – and treat neural dynamics occurring on a number of spatial and temporal scales.
Below is a quick taste of several projects currently underway; we wrote this SIAM News article with another view.
For more, please check out this summary of our ongoing and recent research!
COOPERATIVE NEURAL DYNAMICS AND CODING
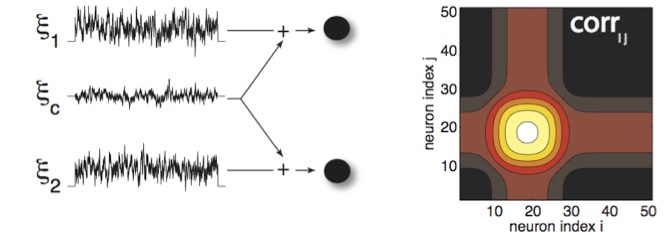
On the left is a schematic that typifies almost any biological neural network: cell pairs receive overlapping inputs, leading to correlated spiking. The transfer of correlated inputs into correlated spikes is strongly modulated by the nonlinear dynamics of neural spike generation. As a consequence, overlapping input can lead to rich patterns of coooperative neural firing across neural populations, as shown on the right. This can have major consequences for levels of encoded information.
Of course, the pictures above are just the tip of the iceberg. Real circuits produce cooperative firing across whole populations of cells, and these cells are connected with rich architectures. Our work on the dynamics of neural correlations and their impact on coding is in collaboration with Fred Rieke, Jaime de la Rocha, Brent Doiron, Kreso Josic, and Alex Reyes -- and within our group, Nick Cain, Yu Hu, Natash Cayco-Gajic, and David Leen are currently pursuing these topics.
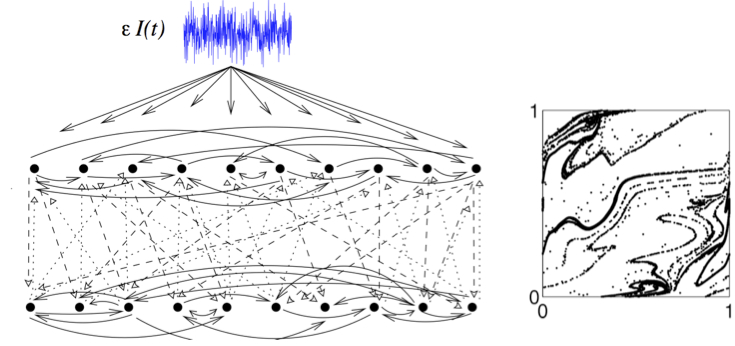
A natural question is: if a neural network receives the same input signal I(t) several times, but starting from slightly different initial states, will it nonetheless produce the same dynamical response -- following a brief transient during which the network entrains to the input? This the question of neural reliability, on which we've worked with Kevin Lin and Lai-Sang Young. Interestingly, the answer is that networks are often NOT reliable -- on the right is Kevin's beautiful picture of a random strange attractor which, rather than entrainment, governs the responses of surprisingly simple model networks. Guillaume Lajoie is spearheading our group's current efforts to extend these results to sparse, randomly connected networks of excitable cells.
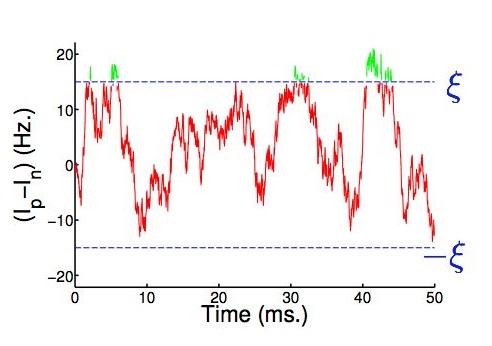
We use highly idealized network models to ask how different circuits accumulate incoming information over time in basic sensory decision tasks. Our work centers around optimality of these circuits -- what mechanisms they would need to implement optimal statistical tests, and what signatures they would produce if these mechanisms were not fully implemented.
Our current research on this problem in collaboration with Michael Shadlen, Nick Cain, and Andrea Barriero. We've worked with Phil Holmes, Jonathan Cohen, Rafal Bogacz, Mark Gilzenrat, and Jeff Moehlis, and many wonderful collaborators on these topics along the way!
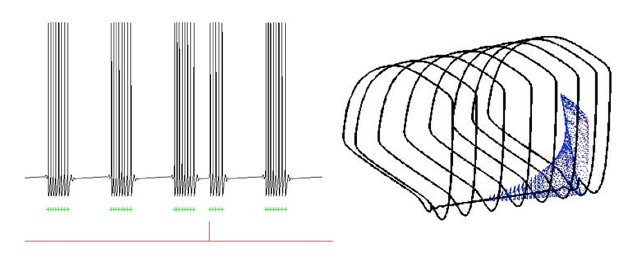
The question posed above arises in two contexts. The first is classic in nonlinear dynamics: oscillators can entrain to their inputs, or display unstable, unpredictable responses. The second is rising in neurophysiology: will a common external drive synchronize or desynchronize a pool of neurons? Above, responses of a model STN cell to pulsatile stimulation (left) depend on whether impulses perturb trajectories past separatrices in the phase space of the model (right). This can split nearby orbits, and we are exploring whether this is behind unstable dynamics that emerged in our earlier studies that sought optimal inputs to desynchronize a complex model of Parkinsonian neurons. Current work on this question is in collaboration with Guillaume Lajoie, Megan Lacy, and Adam Hebb, building on our collaboration with Xiao-Jiang Feng and Herschel Rabitz.