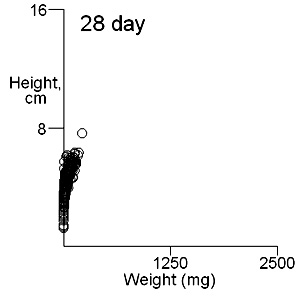
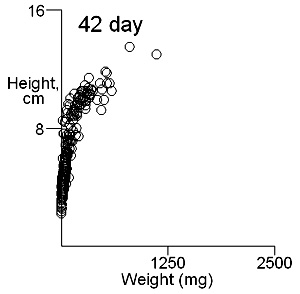
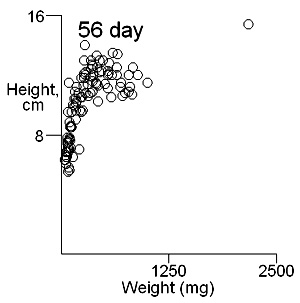
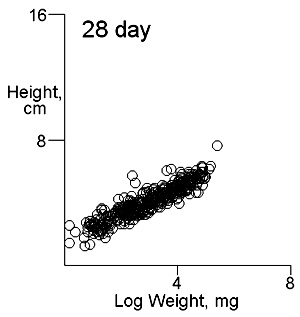
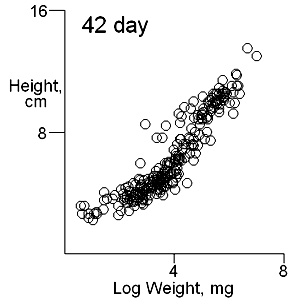
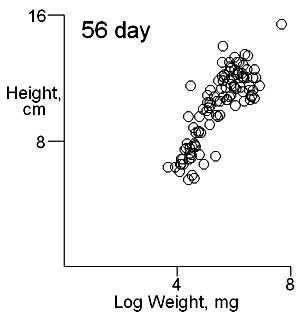
There are two important difficulties in identifying whether multiple modes exist in competition data.   These can result in a tendancy to dismiss the possibility of their existence.  

The first is what measure of plant size to use.   Height may give some indication of the status of a plant in a stand and this is likely to be important where competition is for light.  Weight provides an overall indication of plant success in the competition process.   On previous pages we have shown that height and weight do not necessarily have similar looking histograms and suggest that the relationship between height and weight, or more appropriately for visual comparisons height and log weight, should be studied.    It is also important to consider the development of the population over time.   Below we show the bivariate weight:height and log(weight):height relationshps for three times in the development of stands which gives some insight into the development of stand structure.

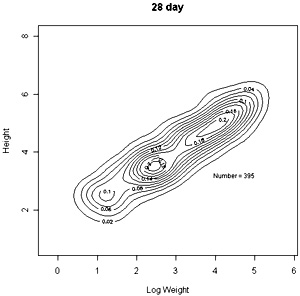
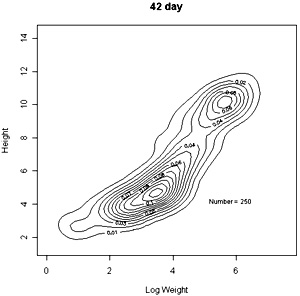
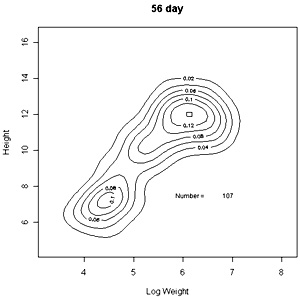
The densities of points in the log weight:height relationships can be represented as follows in contout plots.   Note the differences in scales on the axes in these plots

These contour plots suggest there is development of two modes in the height weight distributions but we should test this by fitting distributions.   There are some important features of these distributions that need to be defined in the fitting proceedure: the modes appear elliptical and there is correlation between height and log weight, particularly at days 28 and 42, and the relationship between height and weight does not seem to follow the same general line, particularly for day 42.  We should also consider how many modes are present.

These aims can be achieved by fitting mixtures of bivariate normal distributions.  Each distribution will have a mean for weight and height, which will define the location of the mode, and a variance between weight and height.  The correlation between height and weight is also defined so that, together with the variances, the elliptical nature of the modes can be estimated. The fitting proceedure also estimates the number of indivuiduals in each mode.

The program for calculating numbers of mode in a bivatiate distribution is written in C so a C compiler must first be obtained.  We have used the lcc-win32 compiler system which is free for non-commercial use.  If you use it professionally you have to have to buy a licence.
  

The method of estimation is by evolutionary computation.  The program first selects values for each parameter and calculates a likelihood for that set of parameters based on the data.  In practice parameter values are created for a population, say of 100 individuals (but this can be varied) so that 100 values of the likelihood are obtained.   The evolutionary computation examines the calculated likelihoods and selects individuals to use in "breeding" a new set of 100 individuals for use in calculations of the next generation.  This process proceeds for a number of generations, say 500 (this too can be varied) and then parameter values that have achieve the greatest likelihood are output.   It outputs that value, along with the parameter values that achieved it, in the paretoset.txt series of files.  The software searches for the set of parameters giving the largest value of likel, that is the least negative.  The program used here is a modification of code first written by Dr. Joel Reynolds (see web site for description and use) and should be cited as:
Reynolds, J.H. and Ford, E.D. 1999. Multi-criteria assessment of ecological process models. Ecology 80: 538-553.

The following files are required.

mult2liknew.c  which drives the calculation and calls the Pareto files.

Four files that calculate the evolutionary computation:
POMAC_breed.c   pomac_main.c     pomac_print.c     pomac_update.c    

Three header files:
pomac_evolve.h     pomac_userconst.h     pomac_userlikeli.h    
  

These C functions are set up to run in the lcc-win32 environment, and although they do not depend on that environment, references to locations of functions are set using it.  A project name must be selected (called here bivariate) with objects and executables in c:\\lcc  The source file mult2liknew.c is placed in c:\\lcc  There are no command line arguments to pass to the program and the start directory is c:\\lcc\bivariate.exe  Then create a new project with objects an executables in c:\\lcc2  and add the remaining C files and header files to it and compile and run.  Output must be tailored to particular needs and the time taken by the program depends upon number of generations and size of the population.  

There are 11 parameters in the bimodal fit used in the mult2lik.c program: Amu1 Amu2 Bmu1 Bmu2 Asig1 Asig2 Bsig1 Bsig2 Acor12 Bcor12 prob
A represents the small size mode and B the larger size, mu1 represents height and mu2 weight (or in the case of this example log weight) and sig represents σ.   cor represents the correlation between height and weight (so Acor12 is the estimated correlation for the small sized (A) mode.   prob is the proportion of the population estimated to be in the A mode.  

The following have to be checked or altered before attempting a search:

• In pomac_userlikeli.h ranges for parameter values are set within which the evolutionary computation searches.   The ranges given in the download version are appropriate for an initial search for the test data supplied.  A guide for ranges can usually be obtained from a contour plot such as those given earlier on this page.  At the end of a calculation it is important to check that the value output for any parameter do not lie at the bounds of its range and to reset the bounds and re-calculate if it does and then check again for all parameters when the calculation has been re-run.

• In pomac_evolve.h the two variables GEN_NUM and POPSIZE need to be checked.  

• In pomac_userconst.h the variables GEN_TO_PRINT needs to be checked.  This controls the number of generations between printing output to file.

• In mult2lik.c you have to set the length of the data by NDATA and the population size to be used in the evolutionary computation search by POP_SIZE.  Smaller values of POP_SIZE give a more rapid size but less evolutionary variation.   

• The two data files are referenced in mult2lik.c  as ht2t.txt for the height data and wt2t.txt for the log weight data.  The file input.txt is used by the evolutionary computation program to store parameter values from generation to generation. You do not have to initialize it.   The critout.txt cotains parameter estimates and a value for the likelihood for the particular set of parameter values listed.