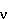) by means of a proportionality constant called Planck's constant
(h). The equation is:
In the following example, we are given one equation that relates
the energy of a photon (E) to its frequency (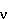
) by means of a proportionality constant called Planck's constant
(h). The equation is:
(I)
We are also told that the speed of light (c) is always equal to
the product of the photon's frequency ( )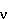
and wavelength ( 
):
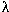(II)
In a typical problem, we might be given the energy (E) of a particular
photon and asked to find its wavelength ( ).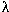
The speed of light c is always known, so we must find a
relationship between what is unknown (the wavelength) and those
quantities that are known (energy and speed of light).
In Eq. (I), we must replace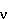
, which is unknown. To do this, solve Eq (II) to obtain
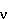an expression for in terms
of 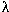and c:
(III) ( (found by dividing both sides of (II) by )
In Eq. (I), replace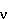
with the above equivalence:
(IV)
Solve Eq (IV) to isolate the only unknown quantity (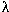
) on the left side:
(V)
(found by multiplying both sides by and dividing both sides by E)
Now substitute in numerical values for h, c, and E into Eq. (V) and you obtain a numerical result for the wavelength .