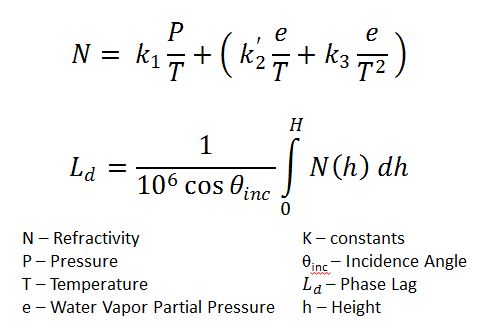Section 1

Mt St Helens Eruption Background

Mount St Helens is most famous for its large, explosive eruption, which occurred on May 18, 1980. The eruption was caused by the catastrophic failure of the volcano’s north flank which had become unstable due to the continued rapid growth of cryptodome on that side of the mountain. After more than a decade of quiescence, Mount St Helens erupted again on October 1st of 2004. The eruption in 2004 was very different from the 1980 eruption and was what is called a dome building eruption. The eruption began with several days of gas and steam explosions, but quickly transitioned to a less explosive state as viscous magma was extruded slowly, building new lava domes within the 1980 crater. This behavior of relatively steady magma extrusion would slowly dissipate and eventually end in the middle of 2008.

In comparison with the 1980 eruption, St Helen’s eruption in 2004 arrived with much less warning. While the 1980 eruption was preceded by both seismicity and surface deformation visible even to the naked eye, the 2004 eruption was preceded only by an increase in seismicity beneath the edifice. It would seem intuitive that the eruption must have been sparked by some sort of increase in pressure at depth, and also that some sort of pressure increase would have been necessary to begin driving a column of viscous magma up through the conduit . Such an increase in pressure would likely have produced deformation observable at the earth’s surface, yet none was detected.

Prior Work

In the years between 1980 and 1991, a large area surrounding Mount St Helens was known to be deforming, resulting in a total of 1-3 cm of uplift. This uplift was measured by trilateration surveys conducted in 1982 and 1991 and was interpreted to be the result of post-eruptive recharge of a deep magma chamber beneath Helens. Interestingly, through the time of the eruption, no further deformation was measured through a synthesis of trilateration data, collected on a broad scale, and campaign GPS surveys conducted in 2000 and 2003, at 17 stations within 5km of the crater. However, if the total displacements from 2000-2003 were small, less than 2 cm, they may have been below the survey’s level of detection. Additional measurements made by a continuous GPS station located at the Johnston Ridge Observatory, approximately 9km away from the crater, did not indicate any surface deformation.

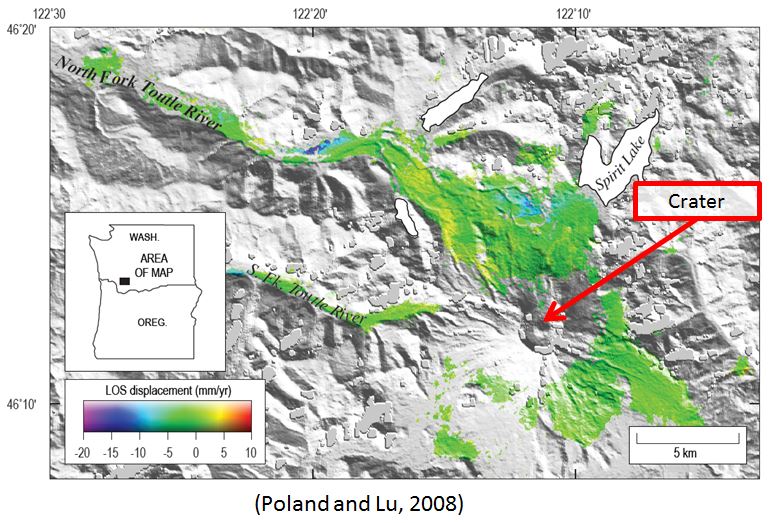
Figure 1. A stack of interferograms made by Poland and Lu (2008) reveals no apparent deformation.
Coherence on the edifice and within the crater is limited due to the presence and disturbance caused by snow.

Because of the wide spatial and temporal spacing, and to a lesser extent, the levels of noise, in data collected by trilateration and GPS, no conclusions could be made about any potential surface deformation that may have occurred locally on the edifice or within the crater of Helens. The ability to produce spatially continuous maps of surface displacements gives InSAR the ability to resolve the question of whether localized deformation may have occurred at Mt St Helens prior to its 2004 eruption. A study conducted by Poland and Lu in 2008 attempted to image both pre and post eruptive deformation at Mount St Helens using interferogram stacking. Because of decorrelation caused by the presence of snow and dense vegetation, even stacks of interferograms were unable to obtain signal within the crater or on the edifice prior to the eruption (Fig 1). While the results prior to the 2004 eruption were inconclusive, post eruptive results successfully imaged subsidence around and on parts of the edifice.

Motivation

Knowing whether or not any deformation occurred at Mount St Helens leading up to its 2004 eruption will augment our understanding of the eruptive cycle at Helens, for instance, what triggered the eruption, and how do we expect magmatic systems beneath volcanoes to recharge through time. The existence and timing of pre-eruptive deformation also has implications on our ability to anticipate future dome-building eruptions at Mt St Helens. It can also help reveal the structure of the magma ‘plumbing system’ beneath Mount St Helens.

There is still potential for InSAR methods to answer the question of whether or not surface deformation occurred at Mt St Helens prior to 2004. The study conducted of St Helens conducted by Poland and Lu (2008) was unable to extract useful data on the edifice because of snow cover and trees, but this problem of decorrelation can be minimized, and in many cases, overcome by newer InSAR processing techniques like Persistent Scatterers methods. If it appears that no measurable deformation occurred on the edifice or within the crater from 1991-2004, one implication, discussed by (Dzurisin et al. 2008), is that the magma which erupted in 2004 finished its ascent by 1991 and was already poised to erupt. Another interpretation discussed is that any magma that continued to ascend after 1991 was accommodated inelastically and did not cause surface deformation. One final possibility is that if a change in pressure or volume at depth did occur, it was too small to be detected by our methods. If a deformation signal is found, and is localized to the edifice or crater, it could be inferred that the change in pressure or volume was shallow, resulting in a more compact signal which would not have been detected by large regional surveys. If detected, the size, shape, and depth of the deformation source can also be investigated through modeling.

Persistent Scatterers Background

Persistent Scatterer (PS) methods (Hooper et al. 2012),(Crosetto et al. 2005), tackle the problem of phase decorrelation by generating a series of interferograms containing a common radar scene and then statistically selecting the pixels with the most stable, or least noisy, amplitude and phase through time. For each pixel in a SAR scene, the phase is an aggregate of the signal generated by all of the scattering elements in the pixel. If a pixel contains a particularly effective scattering element which dominates its signal, like a building, a large boulder, or a rock face, it is more likely to be stable through time. In PS methods, only pixels like these, with the most stable phase and amplitude, are used to generate the final maps of surface displacements and velocities. In this way, the results of PS techniques fully retain any signal from correlated regions and are able to pull reliable information out of the seemingly random areas of interferograms. An unavoidable consequence of PS being a statistical method is that a small fraction of the pixels appearing to be stable are false positives and actually have random phase. Despite this issue, Persistent Scatterers InSAR should vastly improve our ability to detect and measure deformation in the tree and snow covered Cascades.

Persistent Scatterers InSAR Methodology

In this study, the Persistent Scatterer method used is called the Stanford Method for Persistent Scatterers (StaMPS) developed by Hooper et al. (2012). In order to isolate pixels with the least phase noise through time, the StaMPS method begins by choosing the pixels with the most stable amplitude through time as stable. The phase of a pixel in an interferogram can be represented as the sum of the contributions of deformation, changes in the atmosphere, orbital errors, errors in the digital elevation model, and random noise from the instrument and ground scatterers, among other things. The pixels with the least random noise will ultimately be chosen as Persistent Scatterers. In order to solve for the noise of a particular pixel, first the average interferometric phase of all assumed stable pixels within a set distance is subtracted off, removing the spatially correlated signal from deformation, atmosphere, and orbit errors. Next, the DEM error is estimated by least squares, relying on its dependence on perpendicular baseline, leaving only the noise term and some residuals from the previous steps. From these estimates, the pixels with the least variation in noise through time are selected as stable. With an updated guess at which pixels are stable, the process is repeated, yielding lower residuals each time, until the estimates of noise and thus the stability of pixels are satisfactory.

Having determined which pixels are most trustworthy the program returns to the subsampled original interferograms and re-estimates DEM and orbital error terms, and completes phase unwrapping. Finally, in order to estimate atmospheric phase, which is assumed to be spatially correlated and temporally uncorrelated, StaMPS applies a high pass filter in time and low pass filter in space to the data. The atmospheric signal is then removed yielding a set of interferograms, consisting theoretically of only deformation signal and statistically minimized noise and residuals. These interferograms have an improved signal to noise ratio, and can be used to generate time series and maps of average velocity to study surface deformation.

Dataset Description

In this study, the Stanford Method for Persistent Scatterers developed by Hooper et al. (2012) was applied to a set of eight SAR scenes collected by the ERS-2 satellite covering Mount St Helens over the pre-eruptive period, from 1996 to 2002 (Figs 2a, 2b). Many SAR scenes from track 156, frame 2673 were available, but only those from the summer and fall months were chosen in order to minimize the effects of snow. During processing, the number of scenes was further reduced to eight after interferogram pairs having poor perpendicular baselines and high decorrelation were eliminated. Additional SAR datasets from different track –frame combinations exists over Mount St Helens, but are more limited in the time they span, and their number of scenes. Results

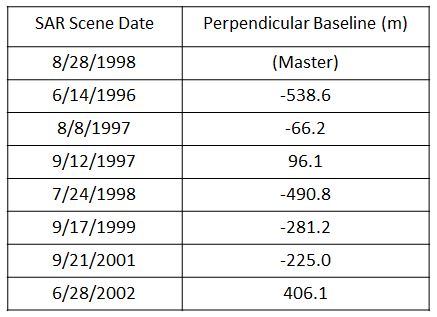
Figures 2(a,b) The map of Washington state on the left shows the location of the SAR scene track 156, frame 2673. StaMPS processing was carried out on a small ~200 square kilometer patch within the frame centered on Mount St. Helens. The table to the right lists the dates of each SAR scene used in StaMPS processing and its perpendicular baseline relative to the master scene.

StaMPS processing was run successfully on the pre-eruptive ERS-2 data, yielding a decent density of stable pixels both on the edifice and within the crater. Refined interferograms were created alongside maps of average velocity over the timespan of 1996-2002. An example interferogram and average velocity map overlain on Google Earth imagery are shown below (Figs 3, 4).

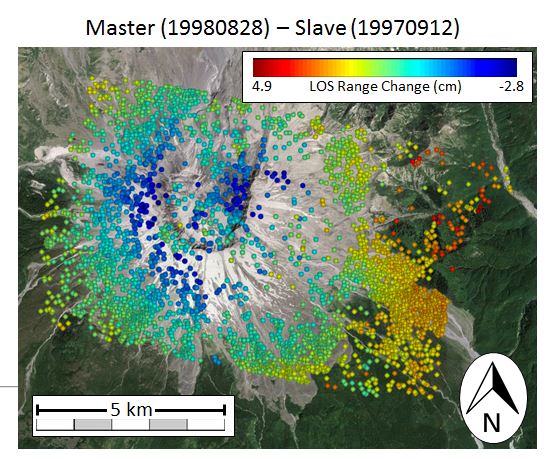
Figure 3. An example interferogram from StaMPS processing, spanning nearly one year from September 1997 to August 1998.
A clear relationship between phase or range change and elevation can be seen in this interferogram indicating contribution from
the atmosphere. Displacements are in the Line Of Sight with red (positive) moving towards the satellite and blue (negative) moving
away from the satellite.

Discussion and Conclusions of StaMPS Processing

Considering the map of average velocities, it can be seen that pixels on the edifice and in the crater are being selected as stable. The phases of the pixels selected over Mount St Helens are spatially correlated to a good degree, indicating that reliable and low noise phase information can in fact be pulled from areas which were decorrelated in previous studies.

Figure 4. Final StaMPS result showing average velocities over the time period of 1996-2002. Apparent uplift signal just
west of the crater is likely an artifact of the atmosphere removal process. Velocities are in the Line Of Sight with red
(positive) moving towards the satellite and blue (negative) moving away from the satellite.

However, there is still much uncertainty about what physical features on the edifice the persistent scatterers correspond to. While it may appear that there is a distinct signal of uplift just off-center of the volcano, there is good reason to believe that the presented results are heavily influenced by atmospheric effects. In several of the interferograms created through StaMPS processing, a strong correlation between phase and elevation was present (Figure 5), indicating influence from atmospheric changes.

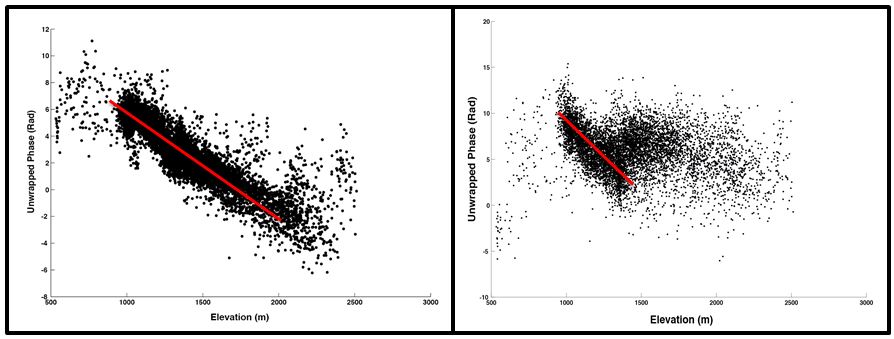
Figures 5 (left) and 6 (right). On the left is an example plot of unwrapped phase vs elevation for an interferogram heavily influenced by the atmosphere. The red line fit to the data is used to create and remove an atmospheric phase screen. On the right is an example of when fitting a line to the phase-elevation data may be subjective or not fully representative of the atmosphere in the interferogram.

In generating the velocity map shown in Figure 4, a tool within StaMPS was used to try and estimate the atmospheric contribution to phase. This tool takes advantage of the fact that the atmospheric contribution to Interferometric phase, is often correlated with terrain elevation. Plots of phase versus elevation are displayed for each interferogram, and the user decides whether and how to fit a line to the data (Figure 5). The linear fit to the data is used to create an atmospheric phase mask which is subtracted from the interferogram after unwrapping phase. In some interferograms, however, the relationship between phase and elevation is less clear (Figure 6), and deciding how or whether to fit a line at all can be subjective, difficult, and substantially impact the final results.

StaMPS processing of SAR data over Mount St Helens identifies pixels with low phase noise on the edifice and within the crater. This indicates that there is promise for Persistent Scatterers processing techniques like StaMPS to overcome decorrelation due to snow and trees and potentially image pre-2004 eruptive deformation. However, because of the possibility that StaMPS results are heavily influenced by atmospheric changes which are difficult to remove using the phase - elevation correlation alone, more work must be done before real signal can be differentiated from artifacts of the atmosphere removal process. It is this fact which motivates the second part of this study: an investigation of the effects of atmosphere on StaMPS processing at Mount St Helens.

Section 2

Introduction

The contribution of changes in the properties of the atmosphere, specifically the troposphere, to Interferometric phase is a substantial obstacle to InSAR studies in many places around the world. The effect of atmospheric phase delay is manifested over a large range of spatial wavelengths and can produce signal of up to tens of centimeters in interferograms (Jolivet et al. 2011). Studying volcanoes with InSAR can be particularly challenging, as both atmospheric effects and surface deformation often correlate with topography and act over similar length scales. In light of these relationships, stacking and the persistent scatterer method StaMPS attempt to remove the contribution of the atmosphere based on the assumption that its changes are not correlated with time, either through temporal averaging or filtering. This assumption may not be sound however, because it has been shown that large portions of the atmosphere are temporally correlated and have distinct seasonal trends (Jung et al. 2014).

In order to more confidently interpret the results of StaMPS processing at Mount St Helens and differentiate between potential deformation and atmospheric effects, I have begun to evaluate the effectiveness of the algorithm for removing atmospheric effects. This has been accomplished by calculating maps of atmospheric phase delay from remote sensing data. I have also started to investigate the spatial and temporal trends in atmospheric phase lag in both a quantitative and qualitative sense.

Dataset Description

The remote sensing atmospheric data used in this study comes from the Moderate Resolution Imaging Spectroradiometer instrument carried by NASA’s Terra and Aqua satellites. A set of 13 MODIS acquisitions spread over the year 2013 were selected to maximize the data coverage and resolution over Mount St Helens. Profiles of various atmospheric properties, including pressure, temperature, and water vapor mixing ratio are collected at roughly five kilometer spacing in a grid-like fashion. Vertical profiles are sampled at between ten and twenty pressure levels within the atmosphere.

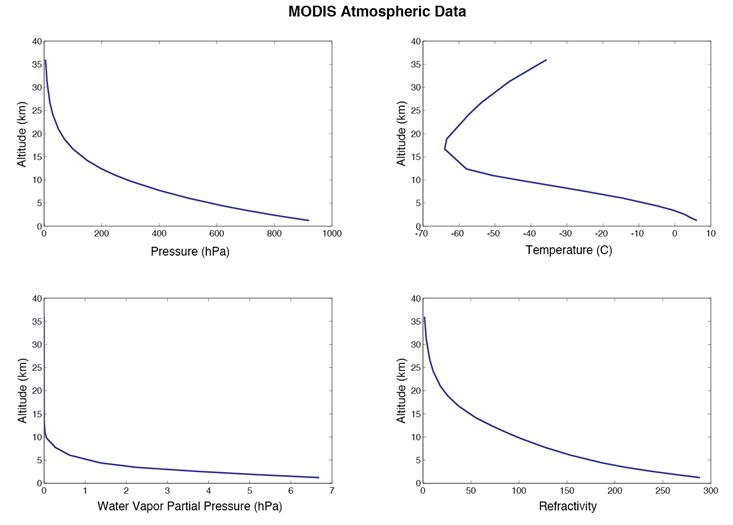
Figure 7. Example MODIS profiles of Pressure, Temperature, Water Vapor Pressure, and Refractivity with respect to Altitude are shown.
The refractivity is integrated from the DEM height to the top of the profile in the calculation of phase delay.

The altitude of each pressure level is estimated for each climate data point. Example profiles are shown in figure 7. The Digital Elevation Model (DEM) used is from the NASA’s Shuttle Radar Topography Mission (SRTM).

Methods

Maps of phase lag for each MODIS acquisition time can be calculated from altitude profiles of pressure, temperature, and water partial pressure (calculated from pressure and water vapor mixing ratio). To calculate phase lag, first a profile of refractivity (N) with respect to height is calculated using Equation 1.

Equations 1 and 2.

The resulting refractivity profiles are then interpolated to the spacing of the DEM using a distance weighted spatial average. Finally, equation 2 is applied to the refractivity profiles, integrating from the DEM height up to an arbitrarily high point, above which there is little atmospheric contribution to phase lag (Jung et al. 2014). An example map of phase lag over Mount St Helens is shown in Figure 8.

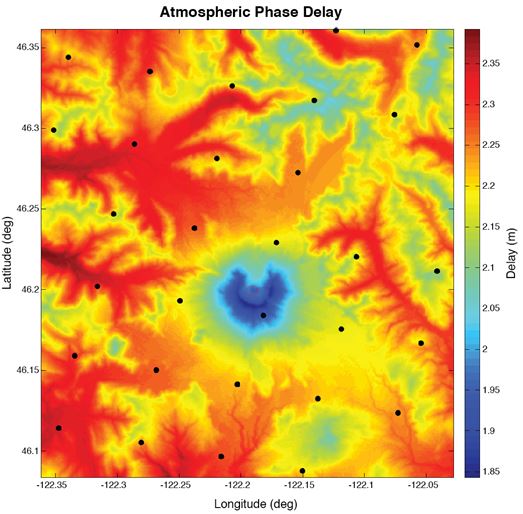
Figure 8. Example map of atmospheric phase delay calculated on a DEM grid covering the Mount St Helens Region. Black Dots spaced at 5km show the locations of the MODIS data points. Mount St Helens is seen as a Blue crescent in the middle of the scene. Red portions of the map experience more delay because they are at lower elevations and the radar will have more atmosphere to pass through.

Atmospheric Phase Screens (APS) depict the difference in phase lag from one time to another and represent the atmospheric component that would be seen in an interferogram. It is important to note that the magnitude of the phase screen at each pixel is relative like phase in interferograms, and that atmospheric phase screens can be simply calculated by subtracting one phase lag scene from another. In this study, the APS calculated from the MODIS data are treated as interferograms containing no deformation or other source of error. A close approximation to the StaMPS processing chain, is applied to APS calculated from the 13 MODIS scenes spanning 2013 to investigate the algorithm’s effectiveness at mitigating atmospheric effects over Mount St Helens.

Results

Maps of atmospheric phase lag like the one shown in Figure 8 are all tightly correlated with topography due to its control of the lower bound of integration in Equation 2 and their magnitudes which are on the order of two meters can vary amounts up 20 cm.

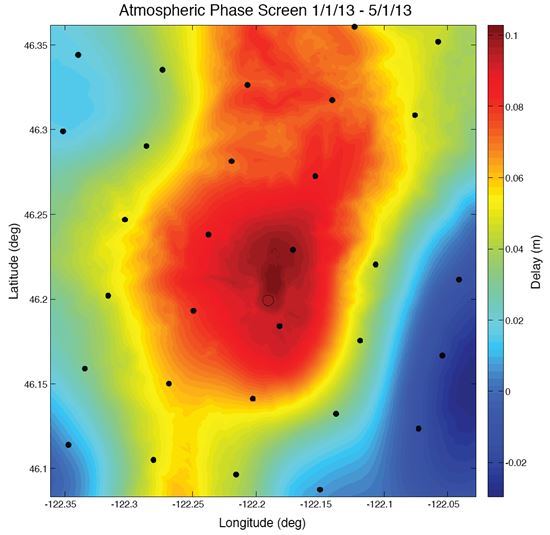
Figure 9. Example of an atmospheric phase screen calculated by subtracting the phase screen for May 1 from Jan 1. In this example, there is a positive (red) delay sitting over Mount St Helens, indicating that more water vapor was likely in the air over Helens on Jan 1 than May 1. Black Dots spaced at 5km show the locations of the MODIS data points. Mount St Helens is centered in the scene.

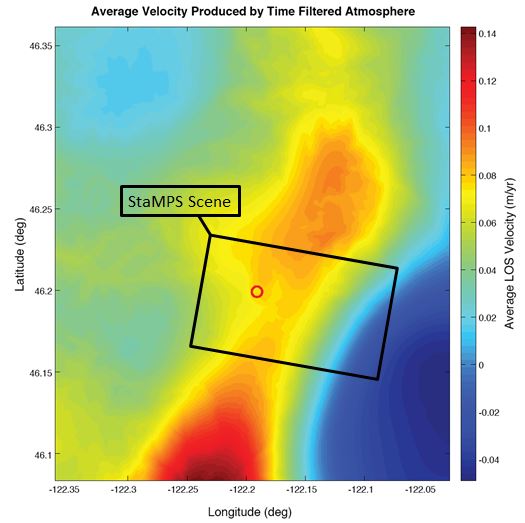
This effect can be clearly seen in an example of APS (Figure 9), where differences in delay of up to 12cm can exist across a scene, arising from differential changes in the water vapor content of the air. Figure 10 shows the map of average apparent velocities that would result from the application of a StaMPS-like algorithm to a series of 12 APS made from 13 maps of atmospheric delay. Differences in velocity on the order of 2 cm/yr are seen over short length scales (~5km), smaller than the StaMPS scene over St Helens (Pictured).

Figure 10. The end result of a StaMPS like algorithm applied to a series of atmospheric phase screens. Gradients in velocity vary across the scene, but are on the order of 2 cm/yr over a 5km distance at Mount St Helens (Red Circle). It is clear from this figure that the applied temporal filtering does not remove all of the atmospheric signal.

Discussion and Conclusions

While this study looks at only a single StaMPS like result, derived from 13 MODIS scenes spanning one year, it seems to be a weak assumption that the effects of the atmosphere are temporally uncorrelated and can be removed by temporal filtering of a time series. For StaMPS studies containing a number of scenes comparable to the 13 in this work, it is likely that an effective low-pass filter in time will find some sort of trend which is manifested as a velocity in a time series. It is also possible that the temporal filter could amplify any apparent average velocity signal by removing the high frequency noise.

With so few atmospheric acquisition dates, it is difficult at this time to make conclusions about spatial and temporal patterns of atmosphere around Mount St Helens. At a minimum, it can be concluded that due to the magnitude of phase shifts caused by atmospheric variations, care should be taken when interpreting the results of single interferograms and even StaMPS results. Additionally, with a low number of SAR scenes, the effectiveness of temporally filtering time-series to remove the atmospheric noise may be insufficient.

Future Work

In the future, much more MODIS data should be analyzed in order to look for seasonal and spatial patterns in phase lag near Mount St Helens. Additional StaMPS-like runs on atmospheric data spanning shorter or longer time intervals than one year, or containing fewer or many more acquisitions could be performed to quantify the ranges of time intervals and number of scenes over which atmospheric changes are handled effectively.

Proposal
Bibliography
Landers Earthquake

Dokuwiki Syntax