Homework 5 –
Answer Set
QSC 482 – Autumn
2002
Prof. Loveday Conquest
Q1)
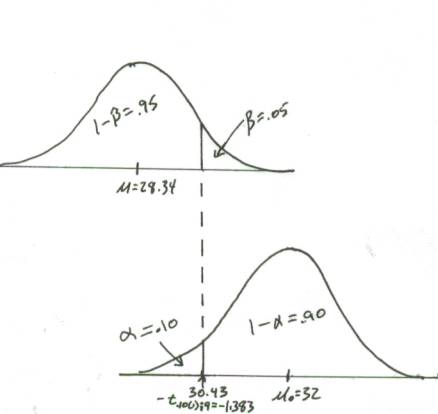
To derive raw score related to –t.10(1);9
= -1.383, note that this value
implies that the raw score value of the cut-off point is 1.383 standard errors
below (negative sign) the hypothesized value of 32. Therefore:
se = s/Ön
= 3.6/Ö10 = 1.138
(t.10(1);9
* se) = -1.383 * 1.138 = -1.57
à 32 - 1.57 = 30.43
To determine m note that here it will be
equal to the hypothesized value (mo=32) minus the MDE (d):
d = (s/Ön)(t.10(1);9 + t.05(1);:9)
= (3.6/Ö10)(1.383 + 1.833) =
3.66 à 32 – 3.66 =
28.34
2a)
Ho: m1-m2
= 0 a
= .10 (two-tailed) n1=6 n2=9 t.10(2);13 =
1.771
Ha: m1-m2
¹ 0
s2p= [(n1-1)s21 + (n2-1)s22]/(n1+n2-2))
= [(5*4.62) + (8*3.52)]/(6+9-2) = 15.6769
sxbar1-xbar2 = Ö(s2p[(1/n1)+(1/n2)]
= Ö(15.6769[(1/6)+(1/9)]) = 2.0868
tobs = |xbar1-xbar2| - d)/
sxbar1-xbar2 = (|40.0-40.5|-0)/2.0868 = 0.2396
Since tobs<1.771, Do Not Reject the null and conclude that the means do not differ.
xbarp = (n1*xbar1
+ n2*xbar2)/n1+n2 = ((6*40)+(9*40.5))/15
= 40.3
(1-a)
100% CI = xbarp - ta(2);n1+n2-2Ö(s2p/(n1+n2))£
m £ xbarp + ta(2);n1+n2-2Ö(s2p/(n1+n2))
= 40.3 - 1.8105 £
m £ 40.3 + 1.8105
= (38.49, 42.11)
2b)
Step 1:
n ³
(2s2/d2)(ta,¥ + tb(1);¥)2 = ((2*42)/.52)(1.6449
+ 0.6745) 2 =
= (128)(5.3796)
= 688.59 à 689
689*2 = 1378 à df
= n1+n2-2 = 689+689-2 = 1376
Step 2:
Since interpolating with an upper bound of ¥
is not really possible, instead just try rounding down degrees of freedom to
next smallest value (i.e., df=1000) and see what happens…
=((2*42)/.52)(1.646
+ 0.675) 2 = 689.541 à 690
690*2 = 1380 à df
= n1+n2-2 = 1378 à STOP
Total sample
size is 690 for each sample for a grand total of 1380.
2c)
tb(1);n1+n2-2= d/Ö(sp2(1/n1)+(1/n2))-
ta;n1+n2-2
tb(1);13= [1/Ö(16((1/6)+(1/9))]- 1.771 = -1.2967
.10<P(tb(1);13£-1.2967)<.25
2d)
Ho: s21=s22
Ha: s21¹s22
F5;8= 3.69
F = 4.62/3.52
= 1.7273
Since
1.7273<3.69 we Do Not Reject the null
and conclude that the variances are not different.
3a)
Test D = Pop1-Pop2
Ho: D£0
Ha: D >0 Ua,n1,n2 = U.10(1);7;9 = 45
|
trace |
1.01 |
1.17 |
1.27 |
1.45 |
1.54 |
1.71 |
1.71 |
1.74 |
1.79 |
1.81 |
1.91 |
2.0 |
2.0 |
2.11 |
2.3 |
|
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7.5 |
7.5 |
9 |
10 |
11 |
12 |
13.5 |
13.5 |
15 |
16 |
R1
= 9+10+11+12+13.5+13.5+15 = 84
R2
= 1+2+3+4+5+6+7.5+7.5+16 = 52
Check:
N(N+1)/2 = 16*17/2 = 136 = R1+R2
U1
= n1*n2+(n1(n1+1))/2)
– R1 = (7*9)+((7*8)/2)-84 = 63 + 28 – 84 = 7 ß Not needed!!!
Note that since this is a one-sided Ha, calculating U1 is unnecessary. We only need focus on R2 since it will be smaller in expected value under Ha (see pgs. 1-10 to 10-13 of class notes). This saves you a little bit of work…
U2
= n1*n2+(n2(n2+1))/2)
– R2 = (7*9)+((9*10)/2)-52 = 63 + 45 – 52 = 56
Umax =
56
Since Umax>45 Reject the null and conclude that the concentration of Am-241 in population 1 does exceed that of population 2.