QSCI 482/Prof. Conquest             TAs Kennedy, Malinick, Norman

 

            HOMEWORK 4 - DUE FRIDAY, NOVEMBER 1, 2002

 

1.  The following data set is a sample of the corvina fish catch

(Sciaenideae) in the "primera" catch category, in kg/boat, from the

Gulf of Nicoya in Costa Rica. It has been speculated that the data

from the nonzero catches are lognormally distributed; that is, the

natural logarithms of the catches follow a normal distribution. 

Here are the original data (in kg/boat-trip):

 

28.7, 145.2, 18.0, 28.2, 7.9, 11.2, 7.4, 3.8, 26.9, 11.4, 6.6, 100.0,

17.8, 2.5, 5.8

 

a. Using SPSS [or your favorite statistical software], do [1] a

histogram of the data and [2] a normal probability plot of the data. 

Examine the histogram for symmetry and "bell-shape" and any extreme

values; examine the normal probablity plot for normality. Give a brief

description of what each plot seems to show.

 

These data appear to be seriously non-normal.  They are heavily asymmetric, right skewed, with a large mode near zero and some data to the right.  The Q-Q plot shows a distinct departure from linearity.  The concavity indicates skewedness.

 

b. Repeat the above (histogram and normal probability plot) on the natural

logarithms of the data. What do you conclude about the characteristics of

the data (catch vs. log catch), by looking at the graphs?

The plots of the new data appear to better approach normality.  The histogram appears fairly bell-shaped and symmetric, and the QQ plot is close to linear.  The log-transformation is definitely an improvement of normality (although still not “perfect”).

 

 

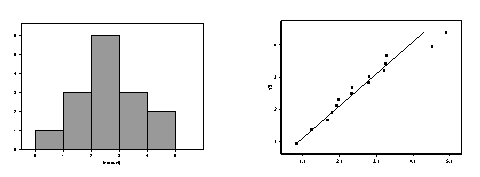
2. Ocean Beauty Seafoods is purchasing new batches of sardines from a

different supplier. Their inspectors are not sure whether the average

length of the sardines from this supplier are the same as or different

from the "old standard" of 4.54 inches. A random sample of n=100 sardines

is drawn from the population, giving a sample mean length of xbar=4.51

inches and a sample standard deviation of s=.23 inches. (You may assume

that sardine lengths follow a normal distribution.)

 

a. At the .05 level of significance, test to see whether the mean length

of the new batches is different from the "old standard" of 4.54 inches.

Include the P-value with your statistical results. What do you conclude?

H0: μ = 4.54; Ha: μ ≠ 4.54.  Data are normal, but σ is not known, so use the t-distribution with 99 df. |t0.05(2),99| = 1.984; Reject H0 if |t|>1.984

 

t=(4.51-4.54)/(0.23/sqrt(100)) = -0.03/0.023 = -1.304

 

|-1.304|<1.984, fail to Reject H0: 0.10 < p < 0.20

The mean length of the new batches is not significantly different from the old standard.

 

b. Compute a 95% confidence interval for the population mean sardine

length of the new batches. Reconcile the result that you get for your

confidence interval with your answer to part (a) above.

 

95% CI: xbar+/-1.984*.23/sqrt(100) = 4.51+/-0.0456

            4.46<=μ<=4.56

      95% CI: (4.46,4.56)

Since the Confidence interval contains 4.54 and 95% of the time our confidence interval contains the true mean, we cannot reject H0: μ=4.54

 

3. A study of littleneck clams (Protothaca staminea) was done in Garrison

Bay, Washington. The following data on variability in shell width was

collected from a random sample of 16 clams:

     

      std. deviation s = 4.6 mm

      n = 16 clams

 

a. Compute a 95% confidence interval for the standard deviation of the

population.

 

           

 

 

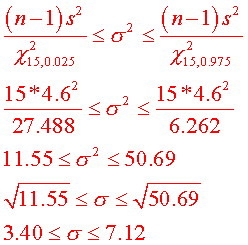
3b. For the littleneck clam data, how large a sample is needed to reject

Ho: mu = 40.0 mm vs. Ha: mu not equal to 40.0 mm if in fact the *true

population mean* mu is really 38 mm? (Use s=4.6 mm, alpha = .10 for

variety, beta = .10.)

 

s=4.6 mm; s2 = 21.16, α = 0.10, β = 0.10; δ = 40-38 = 2.0; δ2 = 4.0;

s2/δ2 = 21.16/4 = 5.29

try   n= ∞: n ≥ 5.29(1.645+1.282)2 = 45.32, round to 46

      n=46: n ≥ 5.29(1.679+1.301)2 = 46.977, round to 47

      n=47: n ≥ 5.29(1.679+1.300)2 = 46.95, round to 47

Sample size n=47 is required.

 

 

 

4. Scientists have conducted studies on the reproductive toxicity effects

of Nitrofen, an herbicide used for weed control in rice and other grains.

Nitrofen is persistent in aquatic systems. Its reproductive toxicity

effects were tested on Cladocera dubia (a zooplankton) at a certain

concentration.

 

a. Suppose we want to compare these data to a *documented standard control

value* of mu=32.0. Even before running the experiment, enough has been

known about Nitrofen to suspect that if Nitrofen does anything at all to

C. dubia, it should *decrease* the average number of offspring.

 

Assuming normality of the data (or at least regarding the behavior of

the sample mean), do a test at the alpha = .10 level to see if there has

been a decrease in the average number of offspring when compared with the

standard control value of 32.0. Be sure to write down the null and

alternative hypotheses. Include the P-value associated with your test

statistic.

 

The data for this part (3a) are as follows: for each of 10 animals, the

number of offspring was recorded, yielding a sample average of 28.3

offspring and a sample standard deviation of s=3.6 offspring.

What do you conclude as a result of your test?

H0: μ ≥ 32.0; Ha: μ < 32.0.  Data are normal, but σ is not known, so use the t-distribution with 9 df.

t0.10(1),9 = 1.383; Reject if t<-1.383

t = (28.3-32)/(3.6/sqrt(10)) = -3.7/1.138 = -3.25

-3.25 < -1.383, so reject H0.  p ~ 0.005

We have enough evidence to say that Nitrofen does decrease the number of offspring of Cladocera dubia relative to the control value of 32.

 

b. If we want to achieve 95% power to test the null and alternative

hypotheses as in part (3a) above, what kind of minimum detectable effect

would we be able to detect statistically? Use alpha = .10, n=10, and use

3.6 as the standard deviation.

α = 0.10; df = 9; β = 0.05; s = 3.6; t0.10(1),9 = 1.383; t0.05(1),9 = 1.833

δ = 3.6/sqrt(10) * (1.383+1.833) = 1.138*3.216 = 3.66